Tuesday’s child is full of probability puzzles
 Subscribe to Decision Science News by Email (one email per week, easy unsubscribe)
Subscribe to Decision Science News by Email (one email per week, easy unsubscribe)
COUNTERINTUITIVE PROBLEM, INTUITIVE REPRESENTATION
Blog posts about counterintuitive probability problems generate lots of opinions with a high probability.
Andrew Gelman and readers have been having a lot of fun with the following probability problem:
I have two children. One is a boy born on a Tuesday. What is the probability I have two boys? The first thing you think is “What has Tuesday got to do with it?” Well, it has everything to do with it.
DSN agrees with Andrew that one virtue of the “population-distribution” method is that it forces one to be explicit about various aspects of the problem, and in so doing, causes much confusion to disappear.
As a public service this week, Decision Science News presents the population-distribution representation of the problem (what it thinks of as the Gigerenzerian / Hoffragian / Peter Sedlmeier-ian representation of the problem) in a visual form.
To follow the logic, see Andrew’s post on how he solved the problem. Voila:
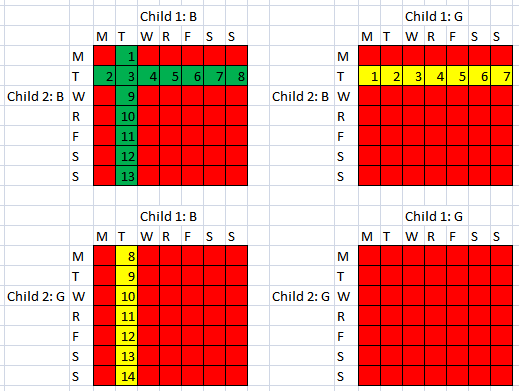
Red means “outside the reference class”. Yellow means “in the reference class but not boy-boy”. Green means “inside the reference class and boy-boy”.
Boy-boy in the reference class occurs with probability Green / (Green + Yellow) or 13 /27
NOTE
To see why DSN calls these Gigerenzerian / Hoffragian / Sedlmeierian representations, see:
Sedlmeier, P. (1997). BasicBayes: A tutor system for simple Bayesian inference.
Behavior Research Methods, Instruments & Computers, 29(3), 328-336.
Gigerenzer, G., & Hoffrage, U. (1995). How to improve Bayesian reasoning without instruction: Frequency formats. Psychological Review, 102,, 684–704.
(Sorry for not using R, excel is just darn fast for some things)


I like solving these things with Bayes’ Rule. It lets you be much more general.
I once worked out the general version of this “one girl was born on a Tuesday” problem:
Consider your friend who has two children…
(Assume throughout that babies are girls with 50% probability, independently.)
Some questions:
0. What is the probabability they have 2 girls?
Pr(GG) = 1/4. That’s 1/2*1/2. Or 1 out of 4 possibilities: GG,BG,GB,BB.
1. What is the probability they have 2 girls given that they don’t have 2 boys?
Pr(GG | not BB), ie, the probability that both are girls given that at least
one is a girl, is 1/3 because now there are just 3 possibilities.
Proof:
Pr(GG | ~BB) = Pr(~BB | GG) Pr(GG) / Pr(~BB) = 1*(1/4)/(3/4) = 1/3.
Or: Pr(GG | GB+BG+GG) = Pr(GB+BG+GG | GG) Pr(GG) / Pr(GB+BG+GG) = 1/3.
2. What is the probability that they have 2 girls given that you ran into
your friend in the park with one of their kids and it was a girl?
Pr(GG | you randomly run into one of the kids and it’s a girl) = 1/2.
The rough intuition is that picking a kid randomly out of a hat is more
informative than just the fact “one kid is a girl”. It’s
counter-intuitive since it seems equivalent to “they’re not both boys”
but the idea is that grabbing a kid at random and seeing it’s a girl is
some weak evidence for GG. If you did that twice (pulled a girl out of
the hat, threw her back, shook up the hat, and pulled a girl out again)
then that’s stronger evidence that it’s GG in the hat. Naturally we’re
assuming that all kids of the same sex are indistinguishable. Naturally.
If you did that several times and kept getting “G” then you’d start to
be convinced that it was GG. Even though all you know for certain is
that they’re not both boys.
Proof:
Pr(GG | G*) = Pr(G* | GG) Pr(GG) / Pr(G*) = 1*(1/4)/Pr(G*) = 1/2 because:
Pr(G*) = Pr(G*|BB)Pr(BB) + Pr(G*|BG)Pr(BG) + Pr(G*|GB)Pr(GB) + Pr(G*|GG)Pr(GG)
= 0 + 1/2*1/4 + 1/2*1/4 + 1*1/4 = 1/2.
Note:
Pr(GG) = 1/4 < Pr(GG | one is G) = 1/3 < Pr(GG | randomly chosen one is G) = 1/2.
And of course,
Pr(GG | oldest is a girl)
= Pr(GG | the one whose name is alphabetically first is a girl)
= Pr(GG | the one who likes jelly beans more is a girl)
= 1/2 (just like Pr(GG | put them in a hat and pull out a girl)).
This makes sense because any of the above imposes an order on the kids
(older / younger, likes jellybeans / doesn’t, the one pulled from hat / the
one still in the hat) and tells you *this* specific one is a girl so the
probability that the other one is a girl is independent — ie, it’s the
probability that any given kid is a girl, namely 1/2.
It turns out that questions 1 and 2 are (roughly) special cases of a more general one:
3. What is the probability that they have 2 girls given that (at least) one of them
is a girl who was born with a quality that occurs in children with probability p?
(For example, if the quality is being born on a Tuesday, then p=1/7.)
In one extreme, if that quality is “born wearing a top hat and singing
A Chorus Line” then p is roughly 0 and one of the kids having that quality
uniquely identifies her. So it’s just like the case where “the older one”
or “the one you ran into in the park” is a girl. Either way, one of the
two kids is uniquely identified and then you’re told she is a girl. So
the probability the other one is a girl is 1/2.
In the other extreme, if that quality is “born on a day that ends in y” then p=1
and question 3 reduces to question 1.
In general, let “Gq” mean a girl who has quality q.
Pr(GG | >=1 kid is Gq)
= Pr(>=1 kid is Gq | GG) Pr(GG) / Pr(>=1 kid is Gq)
= Pr(>=1 kid is q) Pr(GG) / Pr(>=1 kid is Gq)
= (1-(1-p)^2)(1/4)/(1-(1-1/2*p)^2) = 1+2/(p-4).
Eg, for p=1/7 the probability of two girls is 13/27 = ~.481.
Further reading:
http://en.wikipedia.org/wiki/Boy_or_Girl_paradox
http://www.in-gender.com/xyu/Odds/Gender_Odds.aspx
(The real odds and how much the independence assumption is violated.)
Addendum:
What is the probability of 2 girls given that one is a girl named Alice (fraction of girls named Alice is p)?
Pr(GG | >=1 is named Alice) = Pr(GG | A+)
= Pr(A+ | GG) Pr(GG) / Pr(A+)
= 2p 1/4 / (Pr(A+ | BB)/4 + Pr(A+ | GB)/4 + Pr(A+ | BG)/4 + Pr(A+ | GG)/4)
= p/2 / (0 + 2p/4 + 2p/4)
= 1/2.
(The difference between this and “certain quality with probability p” is that names for siblings are not independent.)
May 28, 2010 @ 11:02 pm
Call me a curmudgeon, but I don’t think R stands for Thursday.
May 29, 2010 @ 8:11 am
>Call me a curmudgeon, but I don’t think R stands for Thursday.
R is sometimes used for Thurday. Paste the following into a search engine: M Monday T Tuesday W Wednesday R Thursday
It is funny you say that because one of my Comp Sci profs, another curmudgeon I suppose, said “R stands for Thursday? That’s terrible! You see what happens when you let computer programmers make the decisions? ”
I do confess to being utterly inconsistent in using “S” for both weekend days 🙂
May 29, 2010 @ 2:25 pm
A little trick I picked up from my dad (who picked up the trick at MIT) is to use the symbol theta for Thursday. It’s one letter, and intuitive
May 30, 2010 @ 8:04 pm
Hendrick, Thank you for the best tip I’ve heard in a long time! Did they have a solution for Saturday / Sunday at MIT, too?
May 30, 2010 @ 10:46 pm
I use R for Thursday and U for Sunday, in spite of (or perhaps because of) Andrew’s longstanding scorn for this sort of behavior.
If you want something more elegant, I like Hendrick’s dad’s suggestion of Theta for Thursday. You could also use a lightning bolt; Thursday is Thor’s Day after all. A sun for Sunday would make sense but is too slow to draw, and unfortunately using something that looks like Saturn (for Saturn’s Day) would be damned confusing if you also use Theta for Thursday, since these will look close to identical.
The more I think about it, the more I think R for Thursday and U for Sunday is just fine.
May 31, 2010 @ 3:14 am
How about sigma for Sunday, while we’re using Greek letters?
June 1, 2010 @ 1:33 pm
Reposting this for my friend Jean who posted it on another site:
–begin–
This was a fun problem to think about! And yes, the diagrams did help me understand more quickly the surprising answer than the original text did.
Too bad it’s the wrong answer for real life, since it uses an unrealistic sampling process for that kind of quote. The quote sounds like it comes from a cocktail party rather than a sample conditioned … See Moreby days of the week!
Let me explain the difference with a thought experiment. Imagine a convention of 1000 fathers with two children. Assuming a perfect 50/50 gender breakdown:
250 have two boys (BB)
250 had a girl, then a boy (GB)
250 had a boy, then a girl (BG)
250 have two girls (GG)
Now here are two different ways to sample Tuesdays.
Sample 1, cocktail party: All dads with a boy are asked to raise a hand, and 750 of them do so. We know that of these, 250, or 1/3, have two boys. Next, the 750 dads whose hands are up are told to tell a neighbor which day of the week their son was born. Key part: If they have two sons, they should use the birthday of only one of their sons (randomly chosen). 1/7 of the 500 dads with one son (and one daughter) say Tuesday, and 1/7 of the 250 dads with two sons say Tuesday. So of those who say Tuesday, just 1/3 have two sons. And that’s true of any other day of the week.
Sample 2, raising hands by day of week: Dads with a son born on a Sunday are asked to raise their hands. Next dads with a son born on a Monday are asked to raise their hands. Then dads with a son born on a Tuesday are asked to raise their hands, etc. Note that most dads with two sons will raise their hands *twice*, except for those both sons are born on the same day of the week. This means on any given day of the week, dads with two sons are over-represented relative to dads with one son, since they have two opportunities (one from each son) to have a son born on that day. The diagram demonstrates this over-representation– 13/27th, or 48%, of the dads claiming a son born on a Tuesday have two sons. And that’s true of any other day of the week.
The key difference in cocktail party sampling is that each dad says the birthday of *one* son, even if they actually have two. In the second sampling, the dads with two sons get to raise their hands on *two* days of the week, one for each son (unless the sons were born on the same day of the week).
When most of us hear the quote that started it all, “I have two children. One is a boy born on a Tuesday,” we’re thinking of cocktail party sampling. Someone just decided to tell us about one of their children. So the probability of the speaker having two sons is 1/3. But the answer you gave uses the additional fact of Tuesday as an excuse to change sampling algorithms from cocktail to selecting by day of week, giving the dads with two sons extra representation.
Now my only question is whether you can come up with a clever diagram to represent those two different algorithms of sampling, showing what’s conditioned on what.
To be clear: the key difference between the two sampling algorithms is whether the dads with two sons get to participate once or twice.
We can change the cocktail party sampling so that dads with two sons get to talk to a 2nd neighbor and tell that person the day of the week that their other son was born (if it was a different day of the week). … See MoreIn that case, dads with two sons are again over-represented, and someone who hears “I have a son who was born on a Tuesday” should now infer a 13/27 probability (rather than 1/3) that that dad has two sons.
Or we can change the hand-raising sampling so that dads with two sons can raise their hands only once– randomly picking one son’s birthday. In that case, if you look at the dads with hands raised for Tuesday sons, the probability that one has two sons is 1/3 (rather than 13/27).
So until we live in a world where parents with two sons get to say twice as much as parents with one son, my money is on the 1/3 probability of having two sons when someone tells me, “I have two children, and one is a son born on a Tuesday.”
–end–
June 3, 2010 @ 2:08 am
A little trick I picked up from my dad (who picked up the trick at MIT) is to use the symbol theta for Thursday. It’s one letter, and intuitive
June 4, 2010 @ 12:48 am
[…] a mathematical puzzle posed by Gary Foshee and reported by New Scientist (discussions here and here and here). Gary Foshee, a collector and designer of puzzles from Issaquah near Seattle walked to […]
June 8, 2010 @ 4:46 pm
Forshees calculation is fantastic because it has convinced a whole lot of people that their intutions are completely fooled. But the problem is – the calculations is wrong, but the error is well hidden.
This will explain where the flaw is, and the keys is: Not all outcomes are nessesarily equally weigted:
After the “two children, at least one boy” information we have 3 combinations of the children: BG, GB and BB, as we all probably know. Then let’s merge the weekday information into each specific child combination:
1 – Boy-Girl:
Foshee have told us, that one of the children is a boy, and he’s born on a Tuesday.
In this case it’s 100% certain that his is speaking of the first child, even if the audiences don’t know it (This is actually an important note, as you will see later).
The boy with the specified weekday is called BX (X because it’s irrelevant what weekday the boy is born). So we get these 7 possible combinations: BX-GMon, BX-GTue, BX-GWed, BX-GThu, BX-GFri, BX-GSat and BX-GSun.
2 – Girl-Boy:
Same story: 7 possible combinations: GMon-BX, GTue-BX….
3 – Boy Boy
Now it’s getting interesting. Foshee now have to choose which boy he will reveal the weekday of birth.
BUT – he can only choose one of them! Let’s say Foshee has no preference, so each boy have ONLY 50% CHANCE to be picked.
Each boy delivers 7 combinations (BX-BMon…. and Bmon-Bx…) which gives 14 combinations, but because the chance of each boy to be chosen is only 50%, then the weight of each combination have to be DIVIDED BY 2!
And so the final odds of a 2-boy situation will add up to 1/3 – just as your intuition tells you.
June 10, 2010 @ 10:17 pm
Poul is absolutely correct.
The answer is 1/3.
The trick is based on the indeterminate nature within the BB case – which boy did he refer to? You must not double count the distinct cases.
There are only 7 distinct BB cases, not 13 (or 14). There are 7 BG cases and 7 GB cases. So the correct denominator is 21.
7/21 = 1/3.
Commonsense should tell you that the Tuesday fact has no bearing on the conditional probability in question.
June 18, 2010 @ 8:11 am
Problem 1: Mr. Smith tells you has two children, and at least one is a boy. What is the probability he has two boys?
The mistake almost everybody makes, is that this question is not about Mr. Smith. Probability is a property of a random process, not of a single instance of one – like Mr. Smith. This question is about the random process that brought Mr. Smith’s family to our attention. To solve it, we need to know what that process for everyone, not just Mr. Smith. As stated, it is ambiguous, because it does not tell us what that process is. The problem’s solution is controversial, because different people make different assumptions to resolve the ambiguity, usually without even realizing it.
Here’s the indisputable – because it is also ambiguous – solution to problem #1: Let 0<=B<=1 be the probability that a randomly selected father of a boy and a girl would tell you about the boy instead of the girl. Call that event – that he tells you this fact, not that the fact itself is true – ALOB, for "at least one boy." Using the definition of conditional probability:
P(BB|ALOB) = P(BB and ALOB)/P(ALOB)
= [1*P(BB)] / [1*P(BB) + B*P(BG) + B*P(GB) + 0*P(GG)] = (1/4)/(1/4 + B/4 + B/4) = 1/(1+2*B)
So, if B=1, then P(BB|ALOB)=1/3. If B=1/2, then P(BB|ALOB)=1/2.
B=1 corresponds to a process where every father of two is required to tell us about boys before girls. This requirement is not something you can deduce from what Mr. Smith told you, it is an arbitrary assumption. I personally feel that B=1/2 is the best value to use, for the exact same reason that we say the probability a child is a boy is 1/2. When there are N symmetric outcomes for some part of the random process in a puzzle, we must assign the probability 1/N to each. Since this puzzle gave no reason why a man with two daughters would not say "at least one is a girl," we have to consider that response as a possibility for the PROCESS, but maybe not for this particular Mr. Smith. Since it is symmetric with "one is a boy" for a BG family, in my opinion we have to assume B=1/2, not B=1.
Incidentally, the same logic that leads to 1/3 here, is what leads to 1/2 in the Monty Hall problem. Which the same people will say is wrong.
Problem #2: Mr. Smith tells you has two children, and at least one is a Tuesday boy. What is the probability he has two boys?
The solution (disputable only in what choices to model with variables, and the significant conclusions will not change if you use others) to problem #2: Keep the same B, and let 0<=T<=1 be the probability that a randomly selected father of a Tuesday boy a non-Tuesday Boy would tell you about the Tuesday boy. Counting the cases from the pictures above, of the 196 cases, there is 1 with two Tuesday boys, 12 with one Tuesday boy and a non-Tuesday boy, 14 with one Tuesday boy and a girl, and 169 without a Tuesday boy. Thus:
P(BB|ALOTB) = P(BB and ALOTB)/P(ALOTB)
= [1*1/196 + T*12/196)] / [1*1/196 + T*12/196 + B*14/196 + 0*169/196] = (1 + 12T)/(1 + 12T + 14B)
So, if B=T=1, then the correct probability is 13/27. If B=T=1/2, the correct probability is again 1/2. Even those people who believe that B should be 1 do not find 13/27 intuitive. It's because they universally expect T to be 1/2 regardless of what they feel B is. They refuse to assume that Mr. Smith was required to tell us about a Tuesday boy over a Thursday Boy, or any girl, while making that assumption about "boy" vs. "girl." So, if you think still the answer is 1/3 to both problems, I suggest you examine the reasons you are making the arbitrary assumption that B=1 while you want T=1/2. Why not B=1/2 and T=1, so the answer is 13/20?
June 18, 2010 @ 8:47 pm
Referring to the red and green shaded diagram of the BB matrix above, I am saying that given the statement:
There are 2 children. 1 of them is a boy born on a Tuesday
you can EITHER show this known fact as the green shaded row OR as the green shaded column BUT NOT BOTH.
In the BG case and the GB case, the B is certainly the boy referred to in the statement.
It’s exactly the same for the BB case. The B is certainly ONE of the B’s, but it is not BOTH. Choose one for your analysis. We know nothing about the second B except that the probability of it existing is 1/3, as before.
I hope that helps people resolve the embedded trick.
June 19, 2010 @ 8:31 am
Sam, that is invalid logic, if there is no specific boy referred to. Imagine the actual case is the small box with “3” in it – which boy is “the boy referred to” ?
The person telling us about a family decided to give us incomplete information, applying to only one child. There are several ways he could have decided to do that. He could have picked a two-child family first, and then discovered a fact about them by randomly chosing and describing one child. That leads to the one-row-or-column situation you described, and the answer 1/2 whether or not we are told about the day of the birth. And yes, it is 1/2, not 1/3, because your argument applies to the big boxes as well as the little boxes. If he had picked a girl from a BG family, “at least one boy” is true but he would not have told us that.
OR, he could have first decided to tell us “one child is a boy” or “one child is a boy born on a Tuesday,” and only then sought out a two-child family that the fact applies to. This leads to the answers 1/3 and 13/27, because he is not limited to looking in only the rows, or only columns, for a match. In fact, he is required to look at both, and tell us if he finds a match in either.
Your answer requires a third method. He chooses the fact “at least one boy,” finds a family that matches it, picks a boy from that family (choosing at random if there are two), and then asks what day that boy was born to tell us.
You find the 13/27 answer unintuitive, because the “seek a family that matches the fact” method does not fit well with how the puzzle is presented. The family was clearly selected first. What I’m saying is that this argument applies to both facts – “boy” and “Tuesday” – so the answer should be 1/2 for both questions.
June 19, 2010 @ 12:30 pm
Jeff,
the second child could well be a boy born on a Tuesday too. The point is we know nothing about the second child, neither it’s day of birth or gender. You have been tricked into somehow treating the BB case as different to the GB and BG cases.
It is illogical to double count the BB cases when only one of the axes (column or row) represents the place holder for the actual boy specifically referred to in the original statement.
Yes the place holders switch when regarding BG and GB but this curiosity is merely a logical representational one. It only matters in the BB case where you have to arbitrarily decide which placeholder holds the boy referred to in the statement. Only one can.
June 19, 2010 @ 1:22 pm
No, Sam, the point is that while an individual boy has to be either the first or the second, when you look for a family with a boy you don’t care which you find, so you can find either. Nobody is double-counting anything. Read all of what I wrote, not just one part.
I agree that 13/27 is wrong, but it is wrong for the same reasons that 1/3 is. To get 1/3 you have to look for a family with a boy, but you look at both children so it can be either child. It can represent a row or a column. To get 13/27, you have to look for a family with a Tuesday Boy. Again, you look at both children, and it can be a row or a column.
The answers I expressed in terms of B, or B and T, are right. You just have to decide what B and T are, and they can’t be different.
June 19, 2010 @ 8:50 pm
This may appear repetitive but please read with full critical thinking turned on and bias turned off:
Ann has 2 children sitting on separate chairs behind a screen. She tells you that she has a boy. What is the probability that the other child is also a boy?
Note that Ann’s statement is TRUE. She is saying that of her 2 children, 1 is a boy and for whatever reason she is referring to that particular child. She has told you nothing about the other child, but you know the probability of boy or girl is equal (for our purposes).
We can logically lay out the cases, making sure to keep the instances of children either sitting on the left chair or the right chair:
Ann’s children probability space given her statement:
L R
===
B B
B G
G B
There are only 3 possible arrangements for her children and we see by inspection there is 1/3 probability that there is a second boy behind the screen, the single BB case.
Note that in the BB case, Ann was referring to one and only one of the possible boy children, the one on the left, say. We don’t know which, but we do know that whichever one she was referring to she was NOT referring to the other one. This is fundamental to understanding the problem.
Then Bob comes in and tells us he too has 2 children behind a screen sitting on chairs, and 1 is a boy born on a Tuesday. Bob’s statement is TRUE.
Bob’s children probability space given his statement:
L R
===
B B
B G
G B
Again he is referring to one and only one of his children. He knows what the arrangement is behind the screen, so in either of the 3 mutually exclusive cases above he is referring to either:
1.The boy on the left chair OR the boy on the right chair
2.The boy who happens to be on the left chair.
3.The boy who happens to be on the right chair.
Remember, Bob has complete knowledge about his children. He told you about one of them. The one he IS referring to WAS born on a Tuesday.
But for us trying to assess what is behind the screen all we know is that he is only referring to 1 child. In the BB case, we cannot distinguish which one is the one he is referring to, but we know he refers to only one of them.
The probability of the other one being a boy is therefore unchanged from the Ann scenario when we add some spurious additional information about the child he is already referring to.
You can prove there are only 3 distinct cases by asking Bob to write down which chair the boy he is referring to is sitting, left or right.
Sam
June 20, 2010 @ 6:13 am
Sam, I understand all of what you are saying, and have already pointed out where it is wrong. As I said before, your questions are not about the person you describe in them, Ann or Bob. They are about any parent of two who makes the same statement. Yes, Ann’s statement is TRUE. What is not TRUE is that every mother who CAN make the same statement, WILL make it. Some can, and will, tell you about a girl, or a boy born on a Thursday. The argument you use for days can be used for gender as well. Just apply the difference in rows vs. columns to the four big boxes instead of the 196 little ones.
If Ann is always thinking of a particular child when she says “at least one boy,” then the probability she has two boys is 1/2. The table of all possibilities can be arranged this way:
BB GB
BG GG
If the particular child Ann is thinking of is always listed first (any method that is independent of gender can be used for ordering), then it is clear that our sample space is not:
BB GB
BG
because one of those lists “G” first. It is this, just one column:
BB
BG
This is the exact same argument you are using for the information “born on Tuesday,” but it is applied to the big boxes.
But a mother of two boys does not have to be thinking of a particular boy when she says “I have a boy.” In fact, YOU HAVE TO ASSUME SHE IS NOT to get the answer 1/3. You have to use both rows and columns to get three possibilities for Ann.
The difference you are describing has a name. Say a parent tells us “I have a child who belongs to set X.” We want to define the set S, called the sample space, containing every parent who could be this parent. Clearly, every parent in set S has a child in set X. So X is called a NECESSARY CONDITION for membership in set S. But we do not know whether every child in set X has a parent in set S. We do not know if X is a SUFFICIENT CONDITION for membership in set S.
Your “Ann” question is ambiguous. You are claiming that “boy” is both necessary and sufficient for the S we need. That way, you get 1/3. I am saying it is just necessary, and get 1/2. Neither answer disagrees with anything you said about Ann, just what we assume differently about the Ann’s motivations. You are assuming she is biased toward boys, and I am assuming she is unbiased (and could be thinking about little Annie instead of little Robbie).
Your “Bob” question is ambiguous in the same way. But for some unexplained reason, you are assuming that “boy” is necessary and sufficient, while “Tuesday” is necessary but not sufficient. I am saying that you can’t treat the two conditions differently: either both are sufficient, or neither is. If both are, the answer is 13/27. If neither is, the answer is 1/2.
June 20, 2010 @ 1:29 pm
Jeff
thanks for taking the time to respond. I feel that we are talking at cross purposes.
In deriving a set of all families with 2 children that have a boy with a certain characteristic, of course you are going to select more 2-boy families than naturally occur. That is not what is in dispute. What is in dispute is if you can then draw a conclusion about the gender of the second child based on the fact that 1 is a son born on a Tuesday.
You can prove that there are only 3 possibilities by asking the parent (Foshee) to write down which “seat” the boy he is referring to is sitting on.
Then you say, but his family is in the “set of families selected for this characteristic”. No it isn’t! (based on the information as presented).
There is nothing to suggest that the 2 child family in question is anything other than a binomially distributed family and therefore the chances of there being a second boy are 1/3.
Thoughts?
Sam
June 21, 2010 @ 2:01 am
Who said we want to “deriving a set of all families with 2 children that have a boy with a certain characteristic?” Because that is what Foshee did, and his answer of 13/27 is correct in that case.
We want the set where somebody actually TELLS YOU about the characteristics of one child, but not the other. That’s what makes the difference. There are two issues you are ignoring with that:
1) “Boy” is such a characteristic.
2) You have to distinguish between whether the value of the characteristic was picked first, so the family gets matched to the characteristic if EITHER child has it (what Fochee did); or if the child was picked first and the charcteristic was matched to that child only if that child has it, and is not matched if only the other one does. Which is what you want to do with “Tuesday” bot not “boy.”
Read my original solution. As I said, it in undeniabley correct, and covers the soluiton yuou want. Your answer of 1/3 corresponds to T=1/2 but B=1, which is not reasonable.
June 21, 2010 @ 2:51 am
Jeff
I bow to your superior knowledge.
However, I still am not convinced (due to unfamiliarity with the abstraction you describe).
My assumption is that we are to assess a probability for this instance given some factual information. The given facts have probability of 1. The chances of a parent choosing to mention a boy (born on Tuesday) does not affect what we can do with that information given it has been given (!).
Where do you stop in your random process that gets us to this specific set up?
Sam
June 21, 2010 @ 5:10 am
Sam, you have to remember that the quesiton is about the process, not the specific people mentioned in it. To address that, you may need to know what would happen if the same information could not be given.
There are two ways to use a piece of “factual information” in this puzzle. A parent can be required to mention a child that fact X applies to. But in this case, if fact X applies to neither child, we have no idea what would happen. That’s what makes the problem ambigiuous. Or a parent can choose a child and casually mention a fact Y that applies to that child. Since nothing is required, it doesn’t matter what would happen if fact Y didn’t apply to either. Obviously, the parent would simply choose something else to say.
You are treating “boy” like fact X, and “Tuesday” like fact Y. By limiting your counting to one column only, you are selecting a child and casually mentioning he was born on Tuesday. Had you picked the other child in a two-boy family, the statement would still have been true but we probably would not know it. But you insist that we will always know that a family has a boy, if that is true.
I’m saying that is not consistent. Why not treat “boy” like a fact Y, and “Tuesday” like fact X? Then you get 13/20. No, both facts have to be treated like a fact X, or like a fact Y. If they are treated like a fact X, the correct answer is 13/27. But that means, literally, that the parent is required to tell us “I have a boy born on a Tuesday” if that is true. The answer seems unreasonable, because assuming this requirement IS unreasonable. The only alternative is to treat both facts like a fact Y, and the answer is always 1/2.
What I’m saying is that all the so-called “experts” are wrong when they say the answer to the quesiton, when a parent says “I have at least one boy,” are wrong. The answer is 1/2, unless you know more about why (was it required?) they said that. Martin Gardner admitted this 50 years ago, when he started the controversy about this problem in Scientific American. Kieth Devlin (“The Math Guy” at NPR) admitted the same recently. Most others refuse to address it, but it is true. It is true for the reasons you argue about for “Tuesday,” but you need to apply it to “boy” as well.
June 21, 2010 @ 11:58 am
Jeff
thanks a lot, you’ve helped me clarify where I was being inconsistent.
If I want to argue he was referring to one specific son and he merely added a fact about him, then the other child is equally likely to be G or B: 0.5. As you have repeatedly said.
I only need to reveal the other child behind the screen, I don’t need two chairs (or if I do have two chairs, there are two combinations for BB – I think Devlin shows this with an x for the referred to boy).
I can’t be “Bayesian” for one fact and not the other and remain consistent.
So if you answer 1/3 without the day information, you should answer 13/27 when the day information is provided (simultaneously?).
In the simpler case, if you answer 1/3, you are saying this family is from the set of all 2-child families with at least 1 boy.
When you add the day info, you are saying this family is from the set of all 2-child families with at least 1 Tuesday boy,
Alternatively you can legitimately say the parent was referring to 1 specific child and the chances of the other child being B or G are equal, 0.5 (NOT 1/3 – my error), whatever additional information you add about the referred to child.
Sam
June 22, 2010 @ 1:55 am
Looks like yuou got it. But I’d summarize it:
If you answer 1/3 to the simple question, you are saying this family was selected from the set of all 2-child families with at least 1 boy; that is. Then, for the complex quesiton, you should answer 13/27 because you are saying this family was selected from the set of all 2-child families with at least 1 boy born on Tuesday.
If you answer 1/2 to the simple question, you are saying this family was selected from the set of all 2-child families where a randomly selected child was observed to be a boy. Then, for the complex quesiton, you should answer is the same, because you merely observed more about the selected child.
The question is, which scenario better reflects the questions? How is a parent “selected from the set of all 2-child families with at least 1 boy (born on a Tuesday)?” It uis the unreasonableness of that selection method that causes the strange change in the probability.
June 22, 2010 @ 11:51 am
If we take a random set of two child families, and ask what the probability of two boys is, it is 1/4. This is because the four equally probable outcomes are BB BG GB and GG. Each has a probability space of 1/4 within the set so the total probability in the set is 1.0.
If we then change the set by specifying that at least one of the children is a boy, then the probability of two boys is 1/3. This is because the three equally probable outcomes are BB BG and GB each having a probability within the set of 1/3, again giving a total probability of 1.0
When we look at the diagram representing the Tuesday boy problem, and ignoring the GG quadrant, we have 147 probability spaces (the squares), which we must assume are all equal, at 1/147 probability of the whole set.
Now take the BB square. Every single one of these squares is shared by two days, and therefore you could put a diagonal through each square and write in the two days represented either side of the diagonal. (e.g M/T)
Square 3 in the BB diagram would be marked T/T, and would therefore carry a full 1/147 probability, as would the 6 other equivalent squares for the other days of the week. This would leave however 42 squares where each day carried only 1/294 of the probability.
The denominator for the problem (families with a boy born on Tuesday)therefore becomes 7 BG + 7 GB + 1Boy Tues BoyTues + 12/2 BB = 21.
The numerator becomes 1Boy Tues BoyTues + 12/2 BB = 7
Fraction therefore is 7/21 = 1/3 and all of the probabilities add up to 1.0 within the set. (which they certainly do not with the 13/27 “answer”)
That really is all you need to say about the Foshee problem. The probability is 1/3 for both Problem 1 and the Foshee problem.
June 22, 2010 @ 2:50 pm
Ronosmond: I think you are missing the point.
The reason your argument is wrong is because you can use two different kinds of slashes in each box: one for days (like Tu/Fr) or one for genders (like G/B). So, why does (Tu/Fr) carry only half its normal weight, but (G/B) carries its full weight?
Foshee’s answer is based on the (incorrect, I agree) interpretation that every box has weight 1, but at least it is consistent. (And it “all adds up to 1.” I have no idea what set of “all probabilities” you add up to get something other than 1 in Foshee’s answer, but it isn’t the set Foshee would use.)
Your interpretation is based on (Tu/Fr) having weight 1/2 and (G/B) having weight 1. That corresponds to the statement “I have a boy who just happens to be a Tuesday Child.” That is inconsistent, because you could equally well let (Tu/Fr) have weight 1 and (G/B) have weight 1/2. That makes the answer 13/20, and corresponds to the statement “I have a Tuesday Child who just happens to be a boy.” In other words, you are arbitrarily choosing which way to apply the weights, in order to get the answer you want.
In my opinion, your idea is correct, just applied inconsistently. You do need these weights, but for a slash that divides ALL of the information about the two children inany one box. The combination (B+Tu/B+Tu) gets weight 1, all other boxes that have a single B+Tu get weight 1/2, and all without a B+Tu get weight 0. Then you get 1/2 as your answer. This exactly reflects the information we were given: that the parent could be talking about either child in a (B+Tu/B+Tu) family, only one of the two in a (B+Tu/G+Tu) or (B+Tu/B+Fr) family, and neither in a (G+Tu/B+Fr) family.
June 22, 2010 @ 9:14 pm
JeffJo,
To answer your query:-
To establish the denominator, we are looking for instances of Tuesday boys occurring in two child families.
Each square in the grid gives an example of a two child family, carrying equal probability within the 147 family set (excluding GG quarter).
When we look at the square you quoted Tuesday/Friday, say yellow square 11 in the BG grid, from the point of view of COUNTING CANDIDATES for the denominator, there is no logic in splitting this in two (B/G) as this gives a half share to a GIRL. We are looking for Tuesday BOYS remember, so in this case square 11 counts as a full 1/147 for the only Tuesday boy in that square.
For any square in the BB sector, however, there are TWO Tuesday boy candidates sharing the 1/147 probability.
That is why you can (indeed MUST) split the BB squares in two, and why the BG and GB squares must not be split between Boy and Girl.
The Foshee question is a verbal trick, so we have to pay attention to the wording used. “Tuesday Boy” is a statement about an individual. The Foshee trick is convincing because it applies this statement to a family.
This is the illogical part, but the grid method above allows us to bust open the trick by allocating the correct probabilities to the individual but within the family space allocation.
June 23, 2010 @ 8:33 am
JeffJo
I should have added this;-
To establish the denominator, for each of the 147 equally probable families we ask this question:-
“What is the probability that this family has a Tuesday boy?”
For each of the BG and GB families with a Tuesday boy in, the answer is 100%. Therefore Count 1 for each instance.
For the BB families it is 50%. Therefore Count 1/2 for each instance.
The denominator then becomes 21, and the numerator similarly becomes 7.
June 23, 2010 @ 9:41 am
JeffJo
The tricky thing about this puzzle is getting the English correct.
My question in my last comment was lax, and should have been:-
“What is the probability of the boy in this family being born on a Tuesday?”
This question more accurately reflects the Foshee statement.
June 23, 2010 @ 11:33 am
No, Ron, each square does not carry equal weight with you . It does for Foshee – that’s why he gets 13/27, because he has 13 equal-weighted boxes in green, and 27 equal-weighted boxes in green or yellow.
There are 198 boxes, not 147. You eliminated 169 (not 49) by assigning a weight of 0 to them, because they had no Tuesday Boys. You then assign the weight 1/2 to just certain ones that have only one Tuesday boy, and I’m saying that the way you choose that how is arbitrary.
Lets introduce a concept called a “unit” for a probability puzzle. A “unit” is whatever it is that can take on the set of N random values. So coins, dice, and cards are all “units” in popular puzzles. The values that take on are {heads,tails}, {1,2,3,4,5,6}, and {{2,3,4,5,6,7,8,9,T,J,Q,K,A} x {clubs,hearts,diamonds,spades}}. The, the weight of a box is (Number of units with all caluse correct)/(number of units)
You are trying to treat this puzzle as though it has two units, “boy” and “girl,” that can take on seven values each. That’s why you look for a boy first in each box, and give the box a weight of (number of Tuesday Boys)/(number of boys). What I’m saying is, that is arbitrary. You could make “Tuesday” be the unit, and assign a weight of (number of Tuesday Boys)/(number of Tuesdays).
Foshee is misinterpreting the problem, but at least he is consistent. His unit is “Tuesday Boys.”
The correct “unit” in this puzzle is “child.” The values are {{boy,girl} x {Mo,Tu,We,Th,Fr,Sa,Su}}.
The correct answer is that the weight should be (number of Tuesday Boys)/(number of children).
In other words, the question in this puzzle shoud have been “What is the probability the child in this family is a male child botn on a Tuesday?”
June 23, 2010 @ 12:01 pm
JeffJo,
Let us concentrate on the Foshee statement. He says
“I have two children. One is a boy born on a Tuesday. What is the probability I have two boys?”
So when we trawl the 147 families in the grid that have at least one boy the question we need to ask to establish the denominator is:-
“In this family can we declare with 100% certainty that the boy has been born on a Tuesday?” If the answer is “yes” we count one point.
Applying this question the BG and GB families we can say “yes” in 7 cases each. Count one point each towards the denominator. Therefore we get 14 points in total.
The family in BB where both boys have been born on Tuesday also scores one point. Although each boy only gives 50% certainty of a Tuesday birth there are two of them.
Now let us examine the crucial 12 families which include one Tuesday Boy and one boy born on another day of the week. We cannot answer the question “Yes” with 100% certainty because only 50 % of the family has been born on a Tuesday. So we must only score ½ a point.
This gives another 12 x ½ points = 6.
So the total number of families that meet the criterion in the question is 7 + 7 + 1 + 6 = 21
The numerator is the number of these 21 families that has two boys. This is clearly 1 + 6 = 7
So the fraction is not 13/27 but 7/21 because both numerator and denominator have been stripped of the equivalent of 6 families.
So the answer remains 1/3.
This solution has statistical integrity because all of the total numbers match those of the 147 family set, when we add the data for the other six days of the week.
Numerators 7 x 7 = 49 BB families
Denominators 7 x 21 = 147 total families
This integrity does not apply to the 13/27 answer.
7 x 13 = 91 (out of a total of 49 BB?)
7 x 27 = 189 (out of a total of 147?)
You can choose which answer you prefer:-
13/27 – a superficially correct answer which applies a statement about an individual to a family entity and which, as a result, has no statistical integrity.
OR
7/21 – an answer which takes the Foshee statement and applies the statement about the boy within the family probability space and arrives at an answer which confirms the 1/3 figure for the overall family set.
June 24, 2010 @ 11:46 am
Ron, it does no good to keep re-explaining what you think the right answer is, when I have shown repeatedly that I understand what you are saying. And have shown you why it is wrong. Instead, you need to address what I am saying, to see why it is right.
You said: “when we trawl the 147 families … that have at least one boy the question we need to ask … is ‘can we declare with 100% certainty that the boy has been born on a Tuesday?'”
Why is it not “when we trawl the 147 families … that have at least one Tuesday Child the question we need to ask … is ‘can we declare with 100% certainty that the Tuesday Child is a boy?'” There is no justification to choose your “trawling” method over this one.
So again, I tell you there are 14 classifications of children in this question, not two. Each kind is completely equivalent to any of the others, in terms of how its classification relates to the other 13. “Boy vs. Girl” is treated no differently than “Tuesday vs. Friday;” determining one certainly isn’t placed before the other.
Essentially, this is a question of how we sample the data: do we use full inclusion, or random inclusion? Full inclusion means we require every matching family to be counted. Random inclusion means we only count families where a child chosen at random from the family matches. Foshee uses full inclusion for both kinds of information, and gets 13/27. I use random inclusion for both kinds, and get 1/2 (I get 1/2 for the simpler question, too).
You want full inclusion for one, but random inclusion for the other. The question I keep asking you, and that you keep ignoring, is why does gender merit full inclusion, while the day requires random inclusion? Why not reverse that, and use full inclusion for the day, and random inclusion for the gender?
Please, do not re-explain your methods until you address this question.
And BTW, full inclusion essentially means you pre-screen families to require that at least oen is a boy. By pre-screening for B-Tu instead of just B, Foshee artificially favors families with two boys since there are two chances to get a Tuesday, instead of one chance. That’s why the probability changes. I agree that pre-screening isn’t what the quesiton describes, but the same argument applies to the information “boy.”
June 24, 2010 @ 12:43 pm
JeffJo,
If I had more time, I could take up a contrarian position to your quasi-philosophical musings about what Mr. Smith thinks etc., but I am not going to waste my time doing so.
I have set out, as clearly as I can, a considered calculation which tries to match Foshees conditions exactly. I am not going to expand anymore on spurious “alternative” questions.
Except to say this:
Asking questions about individual children gives you totally different probabilities to asking questions about families, even within the same set.
Take the simple BB BG GB set
Probability of a family with two boys = 1/3
Probability of an individual child being a boy = 2/3
That is why you cannot ask the question that you suggested.
What I was hoping for was someone who could mount a simple defence of the 13/27 Foshee answer.
Is there anyone?
June 24, 2010 @ 6:41 pm
That Anonymous above is me- Apologies for omitting my details.
June 24, 2010 @ 6:42 pm
“Take the simple BB BG GB set. Probability of a family with two boys = 1/3. Probability of an individual child being a boy = 2/3.”
That is true, *IF* you have a simple BB BG GB set. It is not clear that we do, which is why your argument is circular. The quesiton I asked does not address your conclusion, but the assumptions you make to reach it, which is why I can ask it.
Foshee’s answer is correct for the exact same kind of “simple” set you describe – only his is a “simple” (B-Tu)(B-Tu), (B-Tu)(B-NotTu or G), (B-NotTu or G)(B-Tu) set. That is the only defense it needs. You are right that this kind of “simple” set is not appropriate, but it is not appropriate for your purposes either.
I have explained this about ten different ways, and have run out of ways to try. Especially if you refuse to even read it.
June 24, 2010 @ 9:49 pm
JeffJo,
With the passage of time, I have had a look at your argument and am prepared to attempt an answer to your query on your terms.
First though, just to address the issue of the “simple question”. You assert that the answer is 1/2, and I can see that this might indeed be the answer instead of 1/3, but I don’t want to go there in this debate.
But I think you will agree that the four grids shown above BB BG GB and GG have equal probability of 1/4, and that if you state that at least one of the 2 children is a boy, then we end up with three equally probable grids of 49 squares each for BB BG and GB. At least that is the assumption I am using.
Each square represents a family. If we split the square with a diagonal we end up with two triangles, each representing a birth on a day. So in yellow square 8 in the BG grid we have a triangle representing a boy born on a Tuesday and another triangle representing a girl born on Monday. This is one family and I don’t think I can break the information down into any more detail.
In that BG grid we have 7 triangles representing Boy Tuesdays giving 3.5 squares of “space” within the 49 square grid. In fact each of the 14 combinations of weekday – child have 7 triangles each or 3.5 squares of “space” each. This totals up to 98 triangles or 49 squares.
It is easy to see that the same is true of the GB grid.
Now consider the BB grid in the same way. We have 14 triangles dedicated to Boys born on Tuesday. This is worth 7 squares of “space each. The same is true for Boys born on all other days of the week, that is they have 14 triangles or 7 squares of space each = 49 squares. So as far as the births are concerned we satisfy the necessity to have a total probability of 1.0 within the grid.
Now consider the Boy Tuesday families that Foshee talks about. It is indisputable that these families occupy 13 square “spaces” out of 49 in the BB grid and when you add the fact that there are 27 family squares altogether in the three grids that include a Boy Tuesday triangle then it cannot be denied that 13/27 is AN answer to the Foshee question.
My argument is that it is a superficial answer with no statistical integrity, and here is why.
Consider the squares of “space” that Boy Monday families occupy within the 49 square BB grid. This is also 13 – why would it be different from the answer for Tuesday? In fact ALL 7 days have 13/49 of space within the 49 space grid. Thus, if you accept that they all have 13 “spaces” then they occupy 91 of those 49 square spaces.
Now, of course this has no integrity, such as we had with the BG and GB grids, where the square “spaces” were shared equally and completely by the 14 child – day combinations.
Look at square 8 again. The Boy Tuesday triangle counts 1 (out of 7) for the birth but ALSO 1 out of 7 for the families with a Boy Tuesday. This is not a problem when it comes to counting up the numerator and denominators of the fraction because the space is not shared with another boy but with a girl.
In the BB grid Foshee counts a square which contains a Boy Tuesday triangle as 1, but would also count 1 for the same square if it has a(say) Boy Monday triangle. So TWO spaces squeezed into one space!
In the BB grid you cannot squeeze 91 spaces into a grid of 49 spacesof the same size. This is because the 91 spaces are NOT the same size as the 49 grid spaces in terms of probability, because 42 of the squares have boys born on two different days. Only by sharing the probability of these 42 squares between the days concerned can you have the total probability space fit into the 49 square grid.
JeffJo – sorry for the length but I hope I have addressed my meaning in your terms – let me know what you think.
June 29, 2010 @ 12:08 pm
No, Ron, my assertion is that the question is ambiguous. But, that 1/2 is a better answer. I assert this for the same reasons of “statistical integrity” you use. That argument applies equally to both kinds of information we have in this problem – the gender of a child, and the day the child was born. And you don’t need to keep re-explaining how you use the grid. I understand it; what I’m saying is that it may not be the right way to use it.
These are conditional probability problems. To solve them, you need to know not just what the condition is (“at least one boy” or “at least one Tuesday boy”), but whether that condition was applied before or after the family was selected. Here’s how you solve the Tuesday problem:
You start with a population evenly divided between fathers of BB, BG, and GB, and pick a man from it. Not the four you described (196 little boxes), just three (147 little boxes). There is no possibility to pick a man with two daughters. Thus, you have determined that “at least one boy” will be true BEFORE you picked him. It always will be true, and you include every family for which it is true.
Then, this man tells us what day his son (never a daughter) was born; if he has two, you let him pick one at random. There is a possibility that he could have a Tuesday boy, but would say “Friday.” You are not including every family for which this fact is true. Those are the six boxes you are removing from the calculation. So, you are determining that “Tuesday” is true AFTER selecting the man.
That is not how Foshee is solving it. For the exact same reasons you are determining “boy” before picking the man, Foshee is determining “Tuesday boy” before picking the man. There is no chance he will pick a family that does not have a Tuesday Boy. It always will be true, and he includes every family for which it is true. Then, his man will always tell us about his Tuesday boy (never a daughter or a Friday boy). So by doing the exact same thing you are, only with all of the information, Foshee divides the general population not into 3 cases, but into 27. An older B-Tu paired with 14 combinations of B or G and one of the seven days, and a younger boy paired with the same fourteen combinations, but removing the one already counted.
The difference in your calculations is those six boxes you removed by applying “Tuesday” after picking the man, where Foshee applied it before. You got 7/21=1/3, and he got (7+6)/(21+6)=13/27.
What I am saying is that both conditions could be applied after picking the man. There is a possibility the man I pick this way will tell us he has a girl, as well as a possibility he will tell us he has a Friday boy. So I not only remove the six boxes you did, I also remove seven more from just the denominator. For the cases the man tells us he has a daughter. And I get 7/(21-7)=1/2.
The problem is ambiguous because ALL OF THESE THREE METHODS fit the description. There is even a fourth, where you apply “Tuesday” before picking and “boy” after. That gives an answer of 13/20. But the 1/2 answer is best, in my opinion, unless the problem provides a reason why we must apply the condition before picking the man. It must tell us why our random choice is CONSTRAINED to have such a child, which is what applying the condition before picking does. Why is it not just a case of the man OBSERVING the gender and day of birth for one child, which is what applying it after picking does.
That is the reason you apply “Tuesday” after picking, because you are treating it as an observation. You are constrained to pick a boy, but are free to observe any boy’s day of birth. I’m saying that you should not be constrained to pick a boy, and can observe both the gender and the day. There is no more “statistical integrity” in constraining “boy” than there is in constraining “Tuesday.”
(If you are familiar with the Monty Hall problem: The incorrect answer of 1/2 is what you get by applying the condition “Door #3 does not have the prize” before the process. The correct answer of 1/3 is what you get by applying it after the process. It’s the same thing here. After is better, unless you know why it should be before.)
June 29, 2010 @ 5:59 pm
JeffJo,
You come over as a very knowledgable person on the subject, but the problem may be that I am several levels below you in terms of understanding.
I am keen to understand the problem, but so far I don’t follow you.
So can we go slower please and take it one step at a time?
Let me go through each stage of my understanding and then you tell me if I am wrong at each stage.
So, the first stage.
I have used the three grids BB GB and BG. I eliminated GG BECAUSE Foshee told us he did not have two girls.
I believe that the 147 family squares in those three grids represent 147 equally probable combinations GIVEN that we must obey the Foshee condition.
Do you agree with me so far?
June 30, 2010 @ 8:11 am
No, I don’t agree so far. I am going to be exceedingly precise with terminology in this response, because your confusion is rooted in the shortcuts you are making by being imprecise. You are confusing “these family types EXIST with equal probability” with “a family of this type COULD BE the one Foshee is talking about with equal probability.” The two statements are not the same.
First, notice that I talk about family types (or squares), not families. That’s what I meant before about my question not being about Mr. Smith’s family. It is about his family type; more specifically, about how many families with the various family types could match the example of Mr. Smith. You even noticed how that distinction is important, because not all BB families with a Tuesday Boy that EXIST are in the COULD BE category. The question I asked you to answer is not about individual children, as you claimed, it is about the family types that EXIST, and whether they COULD BE.
Anyway, to your “first stage.” There are 196 family types, not 147. They all EXIST with equal probability. But not all COULD BE a match to the example with the same probability. The difference is called a condition, as in “conditional probability,” and we need to recognize not just what it is, but how it is applied.
169 of the squares are colored red in the table above. 49 are in the GG box, 84 are in the BG or GB box, and 36 are in the BB box. Families of all of these types EXIST with equal probability, including the 49 types in the GG box. But none of them COULD BE the one Foshee is talking about, becaseu they violate the condition outright. So you need to assign a weight of 0 to all of them. (It’s really a probability, but I’ll call it a weight to distinguish it from the probabilities we ask for in the end.)
What is wrong with your “first stage,” is that you seem to distinguish red families who have a boy from red families who don’t. You ignore the GG ones completely, while “including without counting” all the others. Foshee’s statement does not make that distinction. All of the red squares are equivalent, and it is important to that keep in mind.
Going to the opposite end of the spectrum, there is 1 square (the #3 green) that has two Tuesday Boys. When I draw the table, I color that one blue. If the family Foshee is talking about has this type, there is only one statement of the correct form that can be made about it. It is no longer a question of COULD BE for them, they MUST BE. So the blue square gets a weight of 1.
There are 12 green squares. When you say you only count 6 of them, that is not quite accurate. What you do is assign a weight of 1/2 to all 12 of them, which adds up to 6. You do this because, while the same number of families may EXIST in each green square as in the blue and red ones, there are two statements of the correct form (“Tuesday Boy” and “Otherday Boy”) that can be made about a green family. So only half of the time do you expect Foshee’s statement to be made for one of them. All EXIST, but only half COULD BE. All of them meet the implied condition, but half will have something else said about them. This shouldn’t be anything new to you, it is what you have been saying all along.
And finally, to the 14 yellow squares. The same number of families EXIST in each yellow square as in any of the others. But there are TWO statements of the correct form that can be made about these families: “Tuesday Boy” and “Anyday Girl.” Not just the one you are allowing. So, just like you did with the green squares, you should assign a weight of 1/2 to the yellow squares because only half of them COULD BE Foshee’s family. If you do this, they add up to 7, not 14.
For some reason I can’t understand, you disagree with that last paragraph. You seem to think that “boy” is a different kind of information than “born on a Tuesday” in Foshee’s statement. You put yellow families in the MUST BE category, just like the blue. You think that my Mr. Smith was actually required to mention a boy; but if he has two he is free to mention the day for either boy. And when you discover you can’t make that methodology consistent with a square from the GG box, you try to ignore that box completely. What I’m saying is that you need to know what statements COULD BE made about every family type EXISTS. Including those in the GG box. Since “Girl” must now be possible in the statement, “Friday Girl” is a possible statement for yellow square #12. Just like “Friday Boy” is possible for green #11.
But what you can’t do, is treat the yellow boxes differently from the green. Foshee goes the other direction from what I do: he assigns a weight of 1 to both colors. All families with a Tuesday Boy are MUST BEs. His Mr. Smith is required to mention a Tuesday Boy whenever possible. Applying the condition this way changes the relative probability of having two boys, because a family with two boys is about twice as likely to have a Tuesday Boy as would a family with only one boy. That’s why his answer goes from 1/3 to 13/27.
To sum up, it all boils down to what freedom Mr. Smith has in mentioning facts about his children. You need to recognize that families without a boy exist, so “I have a girl” must be a possibility. It is only if he is required to mention a boy that the answer to the “simple question” is 1/3. If he is free to choose, it is 1/2. When you add in the day, if B, G, Y, and R represent the weights for each color of box based on his freedom, then the probability of two boys is:
P(BB) = (B+12G+36R)/(B+12G+14Y+169R)
So:
1) If Mr. Smith is required to mention a Tuesday Boy whenever he can, then B=G=Y=1, R=0, and P(BB)=13/27. This is Foshee’s solution.
2) If Mr. Smith is required to mention a boy whenever he can, but is free to mention a day for either when he has two boys, then B=Y=1, G=1/2 (because if he has a green family type he could have mentioned a different day), R=0, and P(BB)=1/3. This is your solution.
3) If Mr. Smith is required to mention a Tuesday Child whenever he can, but is free to mention the gender of any Tuesday Child he has, then B=G=1, Y=1/2 (because he could have mentioned a girl), R=0, and P(BB)=13/20.
4) If Mr. Smith is free to mention the gender+day for either child he has, then B=1, G=Y=1/2, R=0, and P(BB)=1/2.
And there is only one question we need to answer to sort out which solution to use: Does saying “One is a child” mean that Mr. Smith was required to mention a child fitting the description, or does it mean he was free to choose a child and describe that child? Solutions #2 and #3 can’t be right, because they answer this question differently for the different kinds of information in the description. Foshee seems to think the description was required, and choose #1. I disagree, because Mr. Smith is just an example of the process, not the process itself, and choose #4.
But at least I reasoned out why I think so. Foshee uses the “requirement” option without justifying it in the least, which completely ignores how conditional probability works. Even worse, Foshee presented this at an event honoring Martin Gardner, who was one of the first people to recognize the ambiguity I describe. Gardner actually retracted his original answer of 1/3 for the simple problem. Foshee ignores that.
June 30, 2010 @ 4:16 pm
JeffJo,
Like I said, let’s go one stage at a time.
Am I right in thinking that all of the 147 squares that are left when you eliminate the GG grid are “family types” that EXIST with equal probability?
June 30, 2010 @ 6:46 pm
But you shouldn’t do just that. Working out an incorrect approach in more detail will not help you to see the problem.
If you “eliminate” any squares, you should “eliminate” all that can’t (not necessarily “won’t”) satisfy Foshee’s statement. That is the 169 red squares. You are left with 14 yellow squares, 12 green squares, and one blue one (the one actually labeled green-3 above).
All of these EXIST in equal probability. But we don’t know for sure that the father in the family will tell us “I have one child who is a boy born on Tuesday.”
June 30, 2010 @ 8:25 pm
JeffJo,
You are not reading my posts. Here is what I said about the yellow squares in BG:-
“In that BG grid we have 7 triangles representing Boy Tuesdays giving 3.5 squares of “space” within the 49 square grid. In fact each of the 14 combinations of weekday – child have 7 triangles each or 3.5 squares of “space” each. This totals up to 98 triangles or 49 squares.”
You said:-
“And finally, to the 14 yellow squares. The same number of families EXIST in each yellow square as in any of the others. But there are TWO statements of the correct form that can be made about these families: “Tuesday Boy” and “Anyday Girl.” Not just the one you are allowing. So, just like you did with the green squares, you should assign a weight of 1/2 to the yellow squares because only half of them COULD BE Foshee’s family. If you do this, they add up to 7, not 14.”
JeffJo,
This is what I was saying. Read it again and you will see that we do agree.
July 1, 2010 @ 1:26 pm
JeffJo,
To follow up I think you object to the way I count the squares to arrive at the denominator. This is probably the offending paragraph;-
“Look at square 8 again. The Boy Tuesday triangle counts 1 (out of 7) for the birth but ALSO 1 out of 7 for the families with a Boy Tuesday. This is not a problem when it comes to counting up the numerator and denominators of the fraction because the space is not shared with another boy but with a girl.”
Therefore there is not a double claim on the denominator (in this case) because it is a mixed sex family.
July 1, 2010 @ 1:56 pm
So are we addressing just your Stage One, or not?
The red squares represent cases where neither triangle in the square has a B-Tu. In these cases, the father cannot make the statement from Foshee’s problem. It does not matter if the square is in the BB box or the GG box, it must be treated the same. So in your Stage One, you either have 196 squares (including all the red ones) or 27 (eliminating them). You can’t have 147.
In the argument you refer to, which I did read, you use triangles differently than I do. You count each green triangle once, but each yellow triangle twice. You said: “Look at square 8 again. The Boy Tuesday triangle counts 1 (out of 7) for the birth but ALSO 1 out of 7 for the families with a Boy Tuesday.” This is fallacious, but I suppose is your Stage Two.
Just like with the red squares, the box doesn’t matter. Each yellow and/or green square counts either once with weight 1/2 (as I would do it) or once as a triangle (as you would). This is because there is one child who is B-Tu in the square, and one who is not B-Tu. One out of two makes the weight 1/2, or the shape a triangle. It does not matter if the “other” is a B-Fr, a G-Tu, or a G-Fr. THEY ALL WORK THE SAME. You do not get to count a yellow triangle twice, for whatever cryptic reason you meant there.
Also, in your argument against Foshee, you supposed what Foshee would count in *different* *problems.* You can’t add probabilities from different problems together, and expect to get 1. Example: Say I flip two coins. In 75% of the cases I will get at least one heads. In 75% I will get at least one tails. That adds up to 150%.
But you can still use the 75% to say that the probability of double heads, given that at least one heads comes up, is 1/3. (25% of the time you get double heads, and 25%/75%=1/3.) This is right as long as you treat “at least one heads” and “at least one tails” two separate problems: one where you look ONLY for heads, and one where you look ONLY for tails. But your argument against Foshee applies the same way to this one about coins. And I hope you recognize what it is equivalent to. 🙂 (Almost, that is – 1/3 is correct here, because I described the process of flipping coins, not the outcome of one set of flips.)
And this is precisely the difference I am trying to explain to you about Foshee’s problem. He is assuming that, to use a lame metaphor, you met the father at a meeting of Tuesday Boys Anonymous. It’s a group that gathers to resolve issues specific to male offspring who were born on a Tuesday. At the start of the meeting, each person must get up and say something like “Hi. My name is John. I have of children, including a boy born on a Tuesday.” If you collect together all of the members of this society who have two children, you will find that 13/27 of them have two boys. That is what Foshee is calculating, and his answer is correct for his assumption.
While that may not be the best interpretation of the actual problem statement, it is better than yours. You are assuming a different group, Boys Anonymous, and assuming that the opening statement is “Hi. My name is John. I have of children, including a boy born on .” It is because you are requigint “boy” that yo counted the yellw triangles twice. If you collect all of the members who say “two” and “Tuesday” here, you will find that 1/3 of them have two boys. If it was Tuesday Child Anonymous, the answer is 13/20.
The reason we get different answers is because the processes we imagine, to go with the example, are different. My question to you is why you would choose a process that is equivalent to any one of these Anonymous societies to represent Foshee’s question?
July 1, 2010 @ 3:09 pm
I didn’t see your second reply. You did “double claim” the denominator. There is no significance to being a “mixed sex” family, than cannot also be applied to being a “mixed day” familiy. Mixed is mixed, and gets counted once regardless of why it is mixed.
In short, nowhere in counting the denominator can you ask just the question “is this child a boy.” The only question you can ask is “Is this child a Tuesday boy.” Because that is the information that describes the possible families the man has. You can’t separate the facts as you want to do.
And the only reason for asking “is this child a boy” in the numerator, is to determine what squares get counted as having two boys. Not for what weight to use (or for whether to count it as a triangle). That has to be the same as in the denominator, for those you count.
You cannot count any box/sqaure/triangle/whatever twice. It either belongs to the event you are counting, or it does not.
July 1, 2010 @ 4:48 pm
JeffJo,
Thankyou for the huge amount of effort you have put in to advance my education on this topic.
I do now understand fully where you are coming from, and I have learned a lot from your output, but I still see the problem from a layman’s point of view.
I start with the “simple” question where we have two children at least one of which is a boy. Although you appear to cast doubt on it, the usual answer to the probability of two boys in that family is 1/3.
Foshee’s answer is counter-intuitive because it suggests that just gaining the knowledge of the birth day of that boy changes the odds of his having a brother. This is not just counter intuitive, as someone else said on another site, it is astrology, and therefore it ain’t right. (This comment would apply by the way if you thought the answer to the simple question was 1/2.)
The problem is that Foshee’s answer can be backed up by the counting of numerator and denominator described in apparently reasonable English.
My point is – How reasonable is the English? The statement that the boy is born on a Tuesday is one about a BIRTH. Yet we are forced into counting FAMILIES which are combinations of births.
Now Foshee’s counting method is crude because, as you say, he counts one family wherever he sees a Tuesday Boy birth. (Or one square counted for every appropriate triangle seen).
My method allows you to count a triangle as a family ONLY when that Boy-Tuesday triangle provides a 100% certainty that this family matches Foshee’s requirements.
In most of the BB families no such certainty exists. Half of the family you are thinking about counting does NOT match Foshee’s requirements, except in the BoyTuesday-BoyTuesday family where the certainty IS 100%. So count 1 for this family and only 1/2 for the other BB’s.
To me, as someone who knows little of Bayesian/Frequentist methodologies, this is a counting method with far more integrity than Foshee’s method.
And by the way it eliminates the astrology, and returns you to the sanity of the 1/3 answer.
JeffJo, I can sense the gavel rising and another “No you’re wrong, Ron” coming on, but this time I won’t be taken down to the cells.
I’m happy with my position.
July 1, 2010 @ 5:18 pm
Well, Ron, I hate to say it this way, but you’re both right and wrong.
Foshee’s answer is correct, FOR WHAT HE IS ASSUMING. Which is that every man who can tell you “I have at least one Tuesday Boy” does so, and those that can’t don’t say anything. It turns out that 27/196 the fathers of two will be able to tell you this. 13/196 will be able to tell you that, and will also have two boys. So the fraction of men who (1) tell you this and (2) have two boys is 13/27. That is the definition of probability.
This is EXACTLY the same assumption and reasoning that leads to the answer 1/3 in the “simple” question. There, you are assuming that every man who can tell you “I have at least one Boy” does so, and those that can’t don’t say anything. It turns out that 3/4 fathers of the two will be able to tell you this. 1/4 will be able to tell you that, and will also have two boys. So the fraction of men who (1) tell you this and (2) have two boys is 1/3.
You are right, this solution does not match the English. But you are wrong because it doesn’t match the English in either case; so if one is wrong, both are. If you take away the assumption that the random father MUST tell you anything, and let him just mention one child, then the answer is 1/2.
And in all three of these cases, which all yield different answers, there is a 100% certainty that a man who speaks fits Foshee’s requirements. Just like the criterion you seemed to think sets you counting method apart. It doesn’t.
What *is* telling, however, is that in Foshee’s method, 100% of the men who can tell you this, do. In yours, some weird fraction that you have never justified do not. The reason you are wrong, is because you taking away the “must” for the “Tuesday” part, but keeping it for the “boy” part. You have given no reason why the English requires it for one, but not the other.
July 1, 2010 @ 8:45 pm
JeffJo,
A while ago, I was just plain wrong. Now I am right and wrong.
I call that progress.
July 2, 2010 @ 10:00 am
No, as I said in my very first reply to you: your idea is correct, just applied inconsistently. The correct idea is that some squares should have a weight of 1/2 (to be counted once, as triangles). But that applies to every square that has exactly one B-Tu, not selected ones.
Foshee makes an implicit assumption that they are all to be weighted 1. It would be better if he recognized it as an assumption, but his answer is correct within that assumption. You recognize the result of the assumption, but refuse to apply what it means to the problem as a whole.
I really do get the impression that you are putting the answer before the solution. You see a way to get 1/3 for both answers, and you are trying to convince yourself and othes that it must be correct. Not because of any logic behind it, but because it gets the answer you want.
July 2, 2010 @ 11:58 am
JeffJo,
You accuse me of trying to use a method of calculation that gives me an answer of 1/3 for both the simple and the Foshee questions. There is a degree of truth in what you say, but there are good reasons for me doing so.
But first of all can I discuss briefly the answer to the simple question. I can see both sides of the argument about whether the answer is ½ or 1/3. But this piece of empirical data from a person who is in the 1/3 camp persuaded me otherwise (repeated here in case the url link does not work):-
http://www.jesperjuul.net/ludologist/?p=1048
“a) We keep flipping two coins simultaneously.
b) If both coins are tails, we flip the coins again.
c) Otherwise, you give me $15 if there is one head, and I give you $20 if there are two heads.
If the probability is 1/2, you will be making money. If it’s 1/3, I will.
Any takers?”
So, working on the assumption that 1/3 is the correct answer to the simple problem, I move on to the Foshee problem. It is perfectly true that 13/27 is an answer to the question.
Using the same method of calculation and weighting, this is a calculation about a two child family that has at least one boy who was born between midnight and noon.
P of two boys if the boy was born between midnight and noon (assuming as always that births occur at regular frequency for both boys and girls etc….) is 3/7.
It is also true that the probability of two boys if the boy is born between noon and midnight is 3/7.
So from this we can conclude that, if a boy is born between midnight and midnight then the probability of a two boy family is 3/7. So a boy born at any time of the day yields a two-boy probability of 3/7.
Yet the same method of calculation tells us, in the simple question, that the two boy probability is 1/3, if the boy exists. The boy’s existence proves he must have been born between midnight and midnight.
These two probabilities, using the same calculation and weighting, are contradictory and prove that something is amiss with the Foshee calculation.
So, we need to look at the question that led to these two answers.
The calculation of the denominator and numerator is NOT just a mathematical process. The defining statement of both the simple and Foshee problems are both about an INDIVIDUAL birth. So the denominator and numerator enquiries, because they ask about FAMILIES and not individuals, have to be worded precisely.
So, what is the precise generic question we must ask to answer both the simple and the Foshee questions? It is difficult but I would suggest:-
“In this family, is there a boy and if there is does he possess the condition stated?”
Count 1 if you answer “yes” for the family being examined.
So for the simple question, you answer yes because there is a boy (and no extra conditional information) – Count 1
For the Boy Tuesday question the BG and GB families count 1 because they meet both the boy and the conditional requirement.
The BB families meet the boy requirement but only half of the boys meet the Tuesday condition.
So count ½.
Except, of course the BtuesBTues family who count two halves = 1.
I can be accused of backing in to the 1/3 answer, but this question attempts to meet the fact that the Foshee statement is initially about a boy, and then about a condition that applies to the boy.
“I have a boy AND he was born on a Tuesday”
July 5, 2010 @ 1:40 pm
JeffJo,
Apologies again – I am the anonymous contributor above
July 5, 2010 @ 1:41 pm
Ron, the question I have been trying to get you to answer all along is related to step B in your problem. Why is it there? You are right, I will not play that game with that step in there. Will you play this one?
A) A third person flips two coins simultaneously.
B) Without reflipping, he tells us “At least one is a …” and truthfully names “heads” or “tails.”
C) If there are two of whichever he mentioned, you give me $20. If there is only one, I give you $15. If the probability is 1/3, you will be making money. If it’s 1/2, I will. Will you play *this* game?
Now, which game do you think better represents Mr. Smith telling you he has at least one boy, and why? I say either one can, but the second is better because nothing FORCED Mr. Smith to mention boys over girls. HE MERELY MADE AN OBSERVATION ABOUT HIS FAMILY. You do not know that he COULDN’T say “I have at least one girl” if that were true, you only know he DIDN’T.
Then, try this variation of your game:
A) We keep flipping two coins simultaneously on a square table, of sufficient size so that the probability a coin lands within one coin’s width of an edge is exactly 1/7.
B) We repeat unless there is a coin that lands on heads that is within a coin’s width of the edge.
C) Once we stop flipping, I give you $15 if there is one head, and I give you $20 if there are two heads. If the probability is 1/3, you will be making money. If it’s 1/2, I will. Will you play this game?
I warn you, the probability that you solve is for, has a Step B that adds “If both are heads, only look to see if the coin with an earlier date is close to an edge. Ignore where the later-dated coin landed.”
Now, can you tell me why that represents Foshee’s question better than my version?
In short, the “simple question” about boys is ambiguous. It has TWO DIFFERENT ANSWERS, based on whether it corresponds to reflipping the coins (looking for boys/heads), or picking whichever of boys/girls/heads/tails is appropriate for each flip. These two procedures correspond to REQUIRING a heads (or a boy), or OBSERVING a heads (or a boy). Either is consistent with the “simple question.” The answer for the first case is 1/3, and for the second is 1/2.
You said “I can be accused of backing in to the 1/3 answer, but this question attempts to meet the fact that the Foshee statement is initially about a boy, and then about a condition that applies to the boy.” No, it is not. There is nothing “initial” about any part of it. It makes a single statement, that includes both “male” and “Tuesday” at the same level. That’s the whole point. Nowhere in the statement is “Boy” required while “Tuesday” is merely observed.
July 5, 2010 @ 6:26 pm
JeffJo,
Your comment is about whether the simple question is 1/2 or a 1/3, and I bow to your superior knowledge of the intricacies involved.
You will recall that I did say that I can see both points of view. After reading your arguments I still can, and you yourself state that there is ambiguity.
I don’t really care, because all along I have been making a different point. Which is that IF Foshee’s calculation of the simple question comes up with 1/3, then the answer to the Tuesday question is ALSO 1/3.
And if it ends up with 1/2, then the Tuesday Boy question is ALSO 1/2.
I noticed that you still don’t comment on my earlier point that saying that knowledge of a boy’s day of birth alters the probability of his having a brother is astrology. Now I notice that you don’t comment on the 3/7 calculation.
Whether or not the answer to the simple question is 1/2 or 1/3 using the Foshee method of counting the denominator, it has to be the same as the probability for the calculation, using the same counting method, of the morning and afternoon boys.
And it is neither! 3/7 does not equal 1/3 or 1/2.
Therefore, the calculation method is flawed.
July 5, 2010 @ 6:58 pm
And that is the part you are wrong about. IF Foshee’s calculation of the simple question comes up with 1/3, then the answer to the Tuesday question is 13/27 because you have to treat both kinds of information the same way. But IF it comes up with 1/2, then the Tuesday Boy question is ALSO 1/2. Because you have to treat both kinds of information the same way.
The other calcualtions you are trying to do are also ignoring this point, and rteally have no meaning.
July 5, 2010 @ 9:59 pm
JeffJo,
So still nothing to say about astrology or the “Morning Boy” question then?
So we have found a mathematical calculation that JeffJo doesn’t want to analyse.
That’s what I call progress.
July 5, 2010 @ 10:08 pm
There are lots of facts you can assess about “the” boy. The important point is whether they are facts you observed about a child you picked independently of whether those facts applied to them, or whether you looked for a child that the set of facts applied to; that is, that you required those facts.
If all facts (including “male”) are treated as observations, the probability of two boys is always 1/2. If all facts are always treated as requirements, the probability changes with each fact you add, and there is no contradiction. But unless the problem statement separates the facts somehow, which Foshee’s statement didn’t do, you can’t mix these modes of treatment.
I don’t know how to get you to see this difference when you haven’t already, but that is what you are missing.
July 6, 2010 @ 1:11 am
JeffJo,
Yes – all very interesting. But what is the answer to this question.?
“A two child family has at least one boy. He is born in a period of the calendar called “a day”.
What is the probability that his sibling is a brother?”
Use the Foshee method of counting.
Is the answer 1/3 or 3/7 or 13/27?
Take your pick. I have many more answers if you want them.
July 6, 2010 @ 8:13 am
Ron, if Foshee had said “I have two children, and one is a boy who belongs to a subset that conprises a fraction ‘q’ of all children,” then the probability of two boys for this man is (2-q)/(4-q). That comes straight from the squares in above: the fraction (2x-x^2) of the BB square, teh fraction x of each of the BG abd GB squares, and no part of the GG square. That is not “astrology,” that is a direct application of these proportion to the prior probabilities for a two-child family, and then a direct application of the laws of probability to them.
So, if q=1/7 (born on Tuesday), then p=13/27. If q=1/2 (child born after midnight but before noon), then p=3/7. I have no idea what you mean by “born in a period of the calendar called ‘a day,'” since that describes all children. But figure out a q for it, and plug it in to get a p.
But while that is the correct answer assuming the solution method Foshee assumes, it may not be the correct solution method.
There. I’ve answered your questions, and all the future ones you might drag up. Now you tell me, why is “Foshee’s statement initially about a boy, and then about a condition that applies to the boy.” I disagree with this statement of yours. What is it you think “initially” means, and why does it apply to “boy” but not the condition? Since it is centrral to why you keep getting 1/3, you must have a reason. But you keep evading the question with these digressions which provide no new ideas.
July 6, 2010 @ 12:31 pm
This discussion is eerily similar to discussions I’ve had elsewhere, with me playing the part of JeffJo. I find the issue fascinating, largely, if you’ll excuse me, because I want to understand why people can’t understand the answer is not generally 1/3, or 13/27 to the Tuesday variant.
The main issue seems to me to be the tendency to solve probability questions by counting the number of possible outcomes and failing to consider that those outcomes are not necessarily equally likely. Here, that logical error is exacerbated because people—including people who know better, like Keith Devlin and Martin Gardner—start with a sample space with equal probabilities, condition on new information, and then fail to realize that the resulting conditional probabilities are not necessarily equal.
Consider the following problem:
There are four houses. House A contains a billion boys. House B contains a billion minus one boys and one girl. House C contains a billion minus one girls and one boy. House D contains a billion girls. You walk up to a house, you can’t tell which, ring the bell, and a boy answers the door. What’s the probability you’re at house A?
The people insisting the answer to the boy-girl problem is 1/3 might answer: Since a boy answered, I cannot be at house D. There are three remaining possibilities, one of which is house A, so there is probability 1/3 I chose house A.
In this version of the problem, though, it should be easier to see why that reasoning generally fails. Given a boy answered the door, is it equally probable you’re at house A or C? What odd assumption about which kid opens doors in houses with at least one boy and at least one girl makes it equally likely we’re at A, B, or C, given a boy answered the door?
July 6, 2010 @ 6:39 pm
JeffJo,
You said:-
“I have no idea what you mean by “born in a period of the calendar called ‘a day,’” since that describes all children.”
Correct, except that, in my particular question, it means all boys who are part of a two child family.
What isthe difference between these phrases, all of which apply to a boy who is part of a two child family:-
A boy who exists.
A boy who is born between 12 midnight and 12 midnight.
A boy who is born on a day of the week
There is no difference because being born on a day ” describes all boys”
And yet, according to the Foshee method of counting numerator and denominator, the P of that boy having a brother is respectively:-
1/3
13/27 and
3/7
So the same method of calculation to tackle the same question comes up with 3 different answers, and many more besides if you decide to cut a day up in various different ways. This cannot be a robust method of calculation.
I think you conceded above that the Foshee method “may not be the correct solution method”, and that is all I have ever contended.
My method of calculation prioritises the boy, because the simple question is only about the boy, whereas the Foshee question merely adds (irrelevant, as it turns out)information about the boy.
My method also gives the same answer (of 1/3) to the simple question as well as all the other divisons and descriptions of a day. Therefore it is far more robust.
If you can think of a better calculation method to bring all these answers into line, then be my guest, but until then I’m sticking with what I have got.
My objection to the Foshee “presentation” is that he claimed that “Tuesday has everything to do with it”, but all his calculation method demonstrates is that any sub-division of a day, or any weekday also have everything to do with it, albeit that they give a huge collection of different probabilities in answer to the same question.
July 6, 2010 @ 7:03 pm
Ron, “addition” is also a method of calculation, too; yet you do not object to getting different answers when you add 1 and 3, and when you add 47 and 345. Your objection is meaningless, except that you again used it to divert attention away from the question I asked you.
You said “Foshee’s statement initially about a boy, and then about a condition that applies to the boy.”
What is it you think “initially” means, and why does it apply to “boy” but not the condition? Since it is central to why you keep getting 1/3, you must have a reason. But you keep evading the question with these digressions which provide no new ideas.
Because the question is not about a BOY, it is about one of two CHILDREN, who is a boy. That’s why I said “born on a day” describes all CHILDREN. I said exactly what I meant.
The child Foshee is talking about has many attributes that can describe it: “boy” is one of them, but so is “born on Tuesday” or “Born in the morning.” Each one of those attributes separates the child from another child who doesn’t have it: boy separates from girl, Tuesday separates from Friday, Morning separates from Afternoon. Stop treating these attributes differently.
July 6, 2010 @ 8:30 pm
JeffJo,
As I’ve remarked before, my admiration for your mathematical ability is boundless. You clearly have an Intelligence quotient well in excess of 150.
My problem is with your common sense quotient.
We have befor us a method (Foshee’s) of calculating probability which gives many different answers for the same question. You have not denied this.
And yet you appear to carry on defending the basic tenets of that method.
To address your question about why I prioritise boys over the time attributes of boys, the answer is because families are made up of humans, not chunks of time.
AND my method gives consistent answers to the simple question and to ANY sub-division of time or other attributes that you want to pin on the boy.
Why on earth would you prefer the Foshee method? Jesper, on the other site, without any apparent irony, claims that the Foshee method is the basis of scientific and academic probability work.
That might just explain the accuracy of the British weatherforecasters.
July 7, 2010 @ 9:31 am
I don’t like Foshee’s method; I just like yours less. He has a method, you don’t. I’ve asked you repeatedly to explain why you do certain things, and you have responded with only evasion.
Each square in the figures at the start of this thread represents a human child, not a boy child. There is no reason to emphasize maleness over femaleness as you do. Period.
July 7, 2010 @ 11:41 am
Jeff Jo
I have (tried to) explain my method and rationale to you extensively on this thread. I don’t believe I have evaded anything. The fact that you don’t like my answers (e.g. on why I prioritise boys over chunks of time) does not mean I haven’t given them). BTW I “emphasise” maleness only because Foshee talks about a boy. Period.
I have proven that the Foshee method is flawed, and offered up another which, although I freely admit might easily be improved upon, nevertheless gives a consistent answer to both the simple question and any question involving sub division of the boy’s attributes. Foshee’s does not.
You are clearly not persuaded, but I have nothing more to offer you at the moment.
July 7, 2010 @ 2:38 pm
What you have been evading: “Families are made up of humans, not chunks of time” is not an answer to the question I asked. It is a reason you hope will support the answer you want to arrive at.
To see that, change the two problems: “I have two children, and one of them was born before noon. What are the chances both were born before noon?” You would say the answer is 1/3, and that does not recognize your difference between humans and chunks of time. I would say 1/2, and that doesn’t recognize it either.
Then, “I have two children, and one of them was born before noon on a Tuesday. What are the chances both were born before noon?” This is the exact same problem as Foshee asked. The answer is either 1/2 (if this statement represents a set of facts I choose to tell about one child of mine) or 13/27 (if I was chosen to tell you about this child because this set of facts applies to one of my children). Yet both facts are “chunks of time”
+++++
The question is about a man who has two children. It mentions two attributes a HUMAN CHILD can have to reduce, in size, the set of families it is about.
One attribute is gender. The HUMAN CHILD can be a boy, or it can be a girl. We assume HUMAN CHILDREN are divided equally by gender; that is, 1/2 are boys and one half are girls.
Another attribute is the weekday of birth. The HUMAN CHILD can be born on any of seven days I label {Mo, Tu, We, Th, Fr, Sa, Su}. We assume each label represent 1/7 of HUMAN CHILDREN.
Neither of these attributes is what Foshee’s problem is “initially about.” It is only “initially about” a HUMAN CHILD. The facts arrive as a set, not individually, or one before the other. They need to be treated the same way.
The probability changes, in Foshee’s answer, because he requires both attributes but asks about the probability of only one attribute. Since a two-boy family is about twice as likely to meet the full requirement, as a one-boy family, they are represented proportionally higher in the set that meetsa the requirement. I’ve expaliend this about ten different ways. It is not rocket science. Try to understand one of them.
July 7, 2010 @ 5:00 pm
JeffJo,
Like I said I’ve nothing more to offer at this point.
I was hoping beyond hope that you would feel the same way.
July 7, 2010 @ 5:41 pm
Re Sunday.
“Dominical” is the somewhat old fashioned adjective describing Sunday, so how about D for Sunday. I like Theta for Thursday, but I think I’d prefer the archaic English “Thorn” if my character set supported it.
July 7, 2010 @ 10:22 pm
Ron, I am a statistics professor. Can you humor me and sketch answers to the following problems? I am trying to understand where you’re coming from, so I can provide more lucid explanations to students.
Apparently you aren’t interested in the four billion kids crammed into four houses. What if we keep it simpler:
Problem 1: There are four urns. One contains two black balls, one contains two white balls, and two contain a white ball and a black ball. You randomly select a ball from a randomly selected urn and see it’s black. What’s the probability you chose the urn with two black balls?
Problem 2: there are seven black balls numbered 1 through 7 and seven white balls numbered one through 7. Two of these balls are chosen completely at random, and with replacement, and placed in an urn. You reach into the urn and randomly select a ball. You see it’s the black ball labeled 3. What’s the probability the other ball in the urn is black?
I assume your answers to both of these questions are 1/3? Can you sketch your reasoning? If it’s not 1/3 to either problem, can you explain how these problems differ from the boy-girl problems, other than that I’ve specified “randomly”?
July 8, 2010 @ 1:31 am
I am not a mathematician or a statistician, and I’m sure I’m going in over my head here, but I spent a lot of time thinking about this today, so bear with me.
Seems to me the reason this solution (13/27) comes out counter-intuitively is the irrelevant imposition of Tuesday into the data set. Try running it this way:
I have two children. One is a boy born on the 4th of July. What is the probability I have two boys?
If I’m doing the arithmetic right, using the same method that gets you 13/27 for the Tuesday question, you’ll get 729 / 1459. (I eliminated the pesky Leap Year. Never cared for it anyway.) So .49965, very close to 1/2.
Now try this:
I have two children. One is a boy born in the AM. What is the probability I have two boys?
The answer to the “boy born before noon” version is 3/7.
Seems like whatever the limiting factor is (Tues, 4th of July, or AM) sets a certain number X of possibilities in play — for Tuesday the X is 7 (the days of the week, for July 4th, it’s 365, and so on. And the final equation is always 2X-1 divided by 4X-1.
But I think that the fact that it can shown to be different every time, depending on the X factor, demonstrates the irrelevance of the factor. I think (holds breath) that the answer is 1/2 — girl or boy.
Hope I haven’t wasted too much of your time. I know I’ve wasted plenty of my own.
July 8, 2010 @ 3:31 am
Chris,
Problem 1. Answer is 1/3 because the only three urns in contention are BB BW and WB. Only one of the three has two black balls.
Problem 2. Answer is 1/2.
The problem here is that you have asked a different question to that in problem 1.
If you REVEAL the colour of the ball, then you know that the other ball is equally likely to be black or white, regardless of the number on it. Black and white balls in this problem are equal in number.
Now let’s assume that you had asked the equivalent question in problem 2 as in problem 1. Which would have been:-
“In the urn we know that one of the balls is black 3. What is the probability that the urn has two black balls?
This time we know that black 3 is in there but we don’t know which one it is.
The Foshee answer is 13/27, because the method he uses says:-
For the denominator count all pairs of balls that include a black 3. This is 27. For the numerator – of these 27 count how many have two black balls. This is 13. So P = 13/27.
My method says:-
Denominator: Ask first if the urn contains a black ball, and if it does, has it got a number 3 on it. This is to cover the 12 outcomes where you have two black balls with different numbers on.
With these outcomes only HALF of the black balls have a 3 on them , so you cannot be certain that the black ball HAS got a 3 on it. It could equally be another number. I score only 1/2 point for this where Foshee scores a full point.
For the Black3/Black 3 outcome, and for all the Black3/white ball outcomes both Foshee and I score one point. For the B3/W outcomes, you know for certain that the black ball HAS got a 3 on it, and no other..
So my denominator becomes 1 (B3/B3) + 14 (B3/W) + 12/2 = 21.
My numerator, likewise is 1 + 12/2 = 7. P = 7/21 = 3.
July 8, 2010 @ 10:44 am
Chris
Typo – the P in the last sentence should read 1/3 obviously.
July 8, 2010 @ 10:46 am
@Warren: No, you haven’t wasted anybody’s time. You are saying, essentially, what I have been saying (I have a masters in applied math) and what Chris says (he is a statistics professor), but it is good to see a non-mathematician say it.
One way to explain the confusion here, is that probability is a very odd field of mathematics. Some fields, like arithmetic, deal with vey concrete concepts that in general are well understood by non-math people. Some, like topology, deal with very abstract concepts and are not well understood. Probability deals with concrete subjects in an abstract way. Most people will understand the concrete parts, but it is hard to get the math people who are not statistics people to acknowledge that they are not applying the abstract parts correctly. Does thant make sense?
And it’s even harder with puzzles, where you are forced to make many assumptions you wouldn’t in real life. You can forget you are making them. To fracture an old metaphor, it is far too easy to sweep the misunderstanding of the abstract part of probability, under the rug of the assumptions needed for a puzzle.
You have taken a step toward bridging that gap. You have acknowledged that there is an abstract concept you don’t fully grasp, and you reasoned out how it should affect the answer without knowing how it gets there. And that this concept is related to how our intuition pringles at the weird answer. Bravo.
@Ron:
The answer to Chris’ Problem #1 is 1/2. And there are two ways you can explain that. One is the argument you used for Problem #2, which applies equally to Problem #1. They are “the same problem,” because Chris did not say “you know one ball is black,” he said that a randomly selected ball was black. Just like in Problem #2 he said a randomly selected ball was Black #7. The difference is that, while “you know one is black” inplies “one is black,” it is not true that “one is black” implies “you know one is black.” Anyway,
Method #1: If you REVEAL the color of just one ball, then you know that the other ball is equally likely to be black or white, regardless of any other information (or lack thereof) you have about it.
Method #2: The reason it isn’t 1/3 is the abstract concept Warren was reaching for. While three urns may be “in contention,” two of them only “contend” half the time. Because half of the time, you will randomly draw a white ball out of them.
Anyway, let’s try to turn this around. Sometimes problems like Chris’ urn problem #2 utilize a third person called a spy. The spy’s job is to look in the urn, and tell you something about the contents. Suppose there are four different kinds of spy in Chris’s Problem #2:
Spy #1 looks at both balls in the urn, and reports to you one of two statements: “There is a black seven” or “There are no black sevens.”
Spy #2 looks at both balls in the urn. If there are any black ones he takes all of them out. He chooses one of them at random, and sees that its number is X. He then reports either “There is a black X” or “There are no black balls.”
Spy #3 looks at both balls in the urn. If there are any sevens he takes all of them out. He chooses one of them at random, and sees that its color is C. He then reports either “There is a C seven” or “There are no sevens.”
Spy #4 pulls one ball at random, observes its color and number, and reports them to you.
Any one of these spies can say “There are two balls in the urn, and there is a black seven.” The probability that both balls are black is different for each. Before you try to calculate that probability, tell us which of these four spies is the equivalent of Gary Foshee in his Tuesday Boy problem, and why.
July 8, 2010 @ 1:11 pm
Added for Ron: Chris’s Problem #1 is a variation of Bertrand’s Box Paradox, or Gardner’s Three-Card Swindle. You can look it up on the internet, but they only use three urns, so you need to adjust.
The classic solution is that there are eight balls (in Chris’s; six in Bertrand’s)you can draw this way, all with equal probability. Four of them (three in Bertrand’s) are black. Two of those (in either version) come from the urn with two black balls. So the probability is 2/4=1/2 in Chris’s, and 2/3 in Bertrand’s.
July 8, 2010 @ 1:24 pm
This is simpler than it appears. If a family has 2 children and order does not matter, there are only 3 options, not 4.
BB
BG
GG
If we know the gender of one child, we have a 1/2 probability on the other. Adding a GB line implicates that order matters, which is not relevant to our puzzle.
If we want to use the urn & ball visualization, there is only one urn with a black ball & a white ball, not two if order does not matter.
As to the original matter, we know with a 1/1 probability that one child is a boy born on a Tuesday. We only need to find the probability of the 2nd child being a boy, which 1/2.
No probabilities need to be calculated for the known child, because it is a known value stated in the problem. The extra information of a Tuesday is unnecessary to the equation. It is a sidetrack to distract you from what you already know. Which is why so many have tried to do probabilities on two children when the question only asked for one.
July 8, 2010 @ 3:18 pm
Sam
It isn’t enough to count options, you need to assign a probability to each as well. Ordering is just a way to do that more easily, sicen you can then count cases that are all equally probable. Yours aren’t. We don’t actually use the order for anything else.
For example, suppose you have two dice: each has five white sides, and one red side. You get the wrong answers if you assume the three combinations {W+W,W+R,R+R} are equally likely, since W+W will occur 25 times as often as R+R. You can get that result by creating an artifical “order” W1, W2, W3, W4, and W5, where it is easy to see that there are 25 combinations of two white results, and only one of two red.
You can use your system of {0 boys, 1 boy, 2 boys}, but you have to change the probabilities to 1/4, 1/2, and 1/4, respectively. Which amounts to the same thing are *keeping* *track* of the the order without using it for anything.
July 8, 2010 @ 4:54 pm
Chris,
I think JeffJo is right about Problem 1., because you did REVEAL the black ball. Therefore 1/2 is the correct answer (I think).
I lazily assumed that you were giving an anology of the “simple” question. That, of course is not the case because for it to be a true analogy, you would have to have the three urns containing BB BW and WB pairs, and then not REVEAL, but merely be TOLD that there is at least one black ball in each of them.
Under those circumstances, the answer would be 1/3, if you asked the question “What is the probability of finding two black balls in any of the urns?”
July 8, 2010 @ 5:24 pm
Ron, thank you for your response. Can you clarify why you think the two problems are in principle different? As JeffJo points out, in both problems you do know that at least one of the balls in urn you selected is black, but in *both* problems the reason you know that is you randomly selected a black ball—the color of one of the balls was revealed to you. With that in mind, is your answer to both problems 1/2?
Incidentally, one advantage of my phrasing over Foshee’s is I give you everything you need to find the answer through experimentation. If you know any programming language or spreadsheet, you can simulate either problem 1 or problem 2. You could also do problem 1 with a bunch of coins.
July 8, 2010 @ 5:54 pm
Jeff, thank you for such a patient and thoughtful answer. I will take my “bravo” and quit while I am ahead.
July 8, 2010 @ 6:23 pm
Ron, sorry, the remark immediately above was written before I saw your response #77.
I am still not sure I understand how you go about solving the Tuesday variant, but I think you should now agree that the most reasonable answer to the simple boy/girl problem is 1/2. Notice you are implicitly interpreting Foshee’s problem as, “The father tells you he has at least one boy, and you know that a father with at least one boy will ALWAYS tell you that he has at least one boy.” Without the clause after the comma, isn’t it possible that a father with a boy and girl truthfully tells you “I have at least one girl”? Saying “I have at least one boy,” given the father was not BOUND to say that if it’s true, is directly analogous to pulling a black ball out of the urn.
Here’s two puzzles getting at the same issue which I think are interesting when considered together:
Problem 3: All two-child houses with two girls are painted pink, all houses with at least one boy are painted blue. You randomly select a blue house. What’s the probability two boys live there?
Problem 4: Houses are painted as in problem 3. You walk up to a randomly selected blue house, knock on the door, and a boy answers. What’s the probability two boys live there?
I would guess that when presented with both puzzles most people would say the answer to both is 1/3. In fact the answer to 3 is 1/3 and the answer to 4 is 1/2 (assuming boys and girls are equally likely to answer the door). That might be surprising because you already knew at least one boy lives in the house in problem 4 before you knocked on the door.
July 8, 2010 @ 6:25 pm
Chris,
The answer I gave to both of your problems was 1/2 (belatedly in the case of Problem 1). The reason for this is that a reveal of the black ball took place in both cases.
I suspect that my second answer at 5.24, the one which corrected my reponse to Problem 1, may not have been visible to you when you posted your comment of 5.54.
Please advise if this is the case.
I think that your phrasing is fine for both problems, but they are essentially different to Foshee’s problems, because in his all you know is that one of the birth events yielded a boy, but you don’t know which.
In yours you announce the colour of one of the balls which is equivalent to announcing that a GIVEN birth yielded a boy.
July 8, 2010 @ 6:32 pm
This has been a fascinating discussion; as one who managed to get an “A” in post-graduate statistics, I still have a terrible time grasping it.
I say the answer is 1/3; but I agree with JeffJo, so I’ll answer his question why I weigh the “boy” one way and the “tuesday” another.
But first, I’ll illustrate his point. “I have a child born on tuesday who is a boy; what is the probability that I have two children born on tuesday?”
I say the answer is 1/7. I assert that now “tuesday” is the important thing, and “boy” is not.
Confusing question: “I have a child born on tuesday who is a boy; what is the probability that I have two boys?”
Now you might well be persuaded to do the “P(2 boys) given (tuesday-boy)”, as opposed to “P(2 boys) given (tuesday);
Now, why I like 1/3? I assume that there was no random selection of the person talking. The person talking chose to talk. And having chosen to talk, they had the ability to frame the question. If they had two girls, they never would have started with “I have a boy”; they would have said “I have a girl; what is the probability that I have two girls?”
So it makes SENSE to me to eliminate the two-girl choices from consideration, as I never had a chance of hearing the statement “I have no boys” — because I didn’t randomly choose the person speaking.
So, why don’t I use the same rule for “tuesday”? Because, a person who stands up and starts this discussion can ALWAYS provide a day when the boy he is mentioning was born. I didn’t choose “tuesday”, and have him tell me “yes or no” — He told me tuesday, having already identified himself as having a boy. No matter what day the boy was born on, the person who chose to stand could say “I have a boy born on “X””.
So “X=tuesday” is a dependent variable, not an independent one. Sure, that is an assumption, but if falls directly from my assumption that the person speaking CHOSE to speak, and chose to make this problem.
To phrase slightly differently. Someone chose to stand up and ask the problem. They HAD to be a person with two children (100%). They then identified the sex of one child — since their child has a 100% chance of having A SEX, whatever sex the chose to reveal was a 100% certainty for one of their children. I say this because otherwise, there was a possibility they would stand up and say “I have two children, and neither is a boy, what is the chance I have two boys (or two girls)?” in the 1st case it’s 0%, the 2nd 100%, and in neither case would the person have EVER stood and said that, so there is 0% probability of that person doing so.
So I have 100% probability that the person who stood had a boy, and 100% probability that the boy was born on SOME day, and 100% probability that the day the person said was the day the boy was born, in this case “tuesday”, but it could have been any day of the week.
So the “tuesday” wasn’t any more useful than saying “the boy was born on a day”. (I think ron was trying to get here, and I hope my way of phrasing it helps explain that).
So sure, if we randomly chose from a room of 2-child fathers, and we asked if they had a boy born on a tuesday, if they answered YES then the probability of a 2nd boy would be 13/27; but the rational interpretation of the problem as given is that a man chose to stand, picked the sex of one of his children, and then told us what day that child was born.
In which case, the answer is 1/3.
July 8, 2010 @ 6:56 pm
Ron, yes, I hadn’t seen your response.
I still don’t understand why you think problem 1 and the simple boy-girl problem are intrinsically different.
Suppose we reword problem 1 to include one of JeffJo’s spies. The spy who tells you about the urn you selected is like the father who tells you about the composition of his family.
Problem 5: As problem 1, except you don’t draw a ball. Rather, a spy looks into the urn you selected and truthfully reports either “I see at least one black ball” or “I see at least one white ball.” If you selected an urn with mixed colors, the spy flips a coin to decide which sentence to utter. In this case, the spy tells you she sees at least one black ball. What’s the probability you selected the urn with two black balls?
Is your answer 1/2? The only difference between this problem and the simple boy-girl problem is I made it clear how the spy decides to give you information in cases in which he has a choice.
July 8, 2010 @ 7:10 pm
Charles: You need to establish two things to support your position. Suppose a FOO has two properties, P1 and P2. Property P1 can have any of the values {A1, B1, C1,…etc.}, and property P2 can have any of the values {A2, B2, C2, …etc.}
First, you need to establish that “I have a FOO with P1=A1 and P2=C2” is logically different than “I have a child with P2=C2 and P1=A1.” I completely disagree that this differnece exists. The English language does not work that way. One attribute is not “more important” just because it is listed first. That would make it impossible for two different attributes to ever have equal “importance.”
But even if there is such a difference, you still need to establish that it means “I was selected to talk to you because I have a FOO whose more important property has a certain value, and then I choose a FOO of mine with that property value at random and chose to tell you its less-important property value, whatever it is.” I also completely disagree with that. Any such differences in how the properties are associated with my and a FOO of mine have to be described explicitly in the problem.
As it is, regardless of any imagined importance, you have to either assume I was selected because I have a FOO with P1=A1 and P2=C2; or that I reported both property values for a FOO I selected at random. And I completely disagree that the statement means I was selected for the first reason.
July 8, 2010 @ 7:33 pm
Charles, I agree with JeffJo’s response, but I’d add:
You acknowledge that a father with two girls is going to riddle us, “I have two children, at least one of whom is a girl….”
Why do you assume that a speaker with a boy and a girl is ALWAYS going to give us the version of the riddle in which he tells us he has at least one boy?
July 8, 2010 @ 7:58 pm
Chris,
Response to # 80.
Your reasoning about Foshee’s words and how to interpret them – I have read all this before, but I don’t get it. I’m taking the puzzle as it reads. You can go mad trying to puzzle out what was in his mind when he said it.
Problems 3 & 4. I totally agree with both answers. Problem 3 is 1/3 because there is no reveal. Problem 4 is 1/2 because there IS a reveal.
This is the answer to your question in the second sentence of #83.
In your problem there is a reveal. In Foshee’s and the simple problem there is not.
As for problem 5 with your spy, it’s all getting a bit complex, but I would say that, because you don’t know which urn the spy is looking at when he says black, then this does not equate to a reveal. I think a reveal has to match a boy or a black ball to a birth event or an urn respectively.
Problem 1 does. Problem 5 and the simple question do not.
So P = 1/3 (I think) for Problem 5
July 8, 2010 @ 8:09 pm
Ron,
My problem with your phrasing is that I don’t contend the person was “selected to talk to me”. I contend that the person CHOSE to talk to me.
I make no assumption about why they chose to talk to me, except that they chose to provide a riddle that was not trivially obvious, meaning they wouldn’t ask a question for which the answer was NEVER or ALWAYS.
Further, Ron, I don’t mean to imply that the order of two probalistic terms matters. I am saying that the order of the terms in english matters. The problem is a spoken one, and therefore I apply what I contend is a rational ENGLISH explanation for how I translate the spoken word into a probabilistic question.
To illustrate just that point, without analogy to the question; If I’m in a room, and someone says “anybody have two children, where one is a boy”, I might well stand up and shout “I have a boy, he was born on a Tuesday”. It is clear the 1st statement was an answer to the query, the 2nd is just me giving additional information; that additional information gives you no more measurement data, because at that point I am merely giving you other facts about the child I already chose to talk about.
I could spend 5 minutes telling you minute details about my boy, and not one of those details would give you the slightest clue as to whether my other child was a boy or a girl.
Remember, in the real problem I didn’t respond to someone asking about a boy; I simply decided to pose a question, and being a person with two children of gender, I could no matter what children I had and what day they were born, equally state the puzzle, “I have a two children, one is gender X born on day Y”.
The only reason the gender becomes important, and not the date, is that the phraseology of the statement implies the gender is important, (because I am asked about the gender of the other child) while the day, which could have been ANY day, seems to be there to throw me off, because I am not asked about the day the other child was born).
This doesn’t make other interpretations of the problem wrong; I simply assert that my interpretation, rather than being the least justifiable as you have asserted, is the most justifiable. You certainly don’t have to agree with me, but I do hope I have at least been able to give you a framework in which you can see how that could be the case.
Chris, I don’t assume that the B/G father will always say “I have a boy”. I merely contend that whichever they choose to tell us doesn’t change the problem in any way. Once we assume only a father with 2 children could start the problem, that father will be able to state the puzzle, and his statement of the puzzle will be entirely controlled by the gender and birth day of one of his children, a choice he makes which is entirely non-random, and which which being dependent variables, should not both be used when determining the outcome based on ONE of the variables.
Which gets me back to the wording of the question; the probability outcome we are to give is clearly based on gender, since it is about one of the gender pairings (boy/boy). The date is dependent on the day the boy he chose was born, and therefore is useless for determining the gender/gender pair; If he asked what the chances were that his other child was born on day “D”, the sex of the boy would be dependent on the child he chose, and would likewise be useless for determining the day the other child was born.
So you choose the variable given based on the outcome being questioned; gender for gender, day for day.
If you instead phrase the question as “You walk into aroom of people with two children, and walk up to one and ask, do you have a boy born on tuesday, and they say “yes” — what is the probability that they have two boys?”, then the answer is 13/27.
Ron,
July 8, 2010 @ 8:46 pm
Charles @ #87,
I think you mean JeffJo instead of me. At least I hope you do,
July 8, 2010 @ 8:51 pm
The Spy Problem (love it):
There are seven black balls numbered 1 through 7 and seven white balls numbered one through 7. Two of these balls are chosen completely at random, and with replacement, and placed in an urn.
For each spy, assume they say “Black Seven”, and provide the probability that there are two black balls.
There are 196 total possibilities, each equally likely.
Spy #1 looks at both balls in the urn, and reports to you one of two statements: “There is a black seven” or “There are no black sevens.”
There are 27 cases of a black 7. b-7, b1-7; b-7, w1-7, w1-7,b7, b1-6, b7. Of those, 13 have two black balls. Probalility 13/27.
Spy #2 looks at both balls in the urn. If there are any black ones he takes all of them out. He chooses one of them at random, and sees that its number is X. He then reports either “There is a black X” or “There are no black balls.”
In this case, if there is a black ball, it will have a number “X”, so “X” is determined and has a probality of 1. There are 147 possible choices with a black ball, and of those 49 have two; so the probability is 1/3. This is my contention for the boy/tuesday problem, with my assertion that “tuesday” was simply the day the boy chosen was born, and not a random selection.
Spy #3 looks at both balls in the urn. If there are any sevens he takes all of them out. He chooses one of them at random, and sees that its color is C. He then reports either “There is a C seven” or “There are no sevens.”
Again, tuesday will have a color “C”, with 100% certainty, whatever that color is. If C was white, the probability of 2 black would be zero, but the assumption is the spy said “there is a black ball with number 7”.
There are 52 choices with at least 1 7; of those, 13 have two white balls, 13 have two black balls, and 26 have a white and a black ball. Sicne the spy said “black 7”, the 13 with two white balls are eliminated. Of the remaining 39, 3 have two 7’s, the rest one 7. Of the 3 with two 7s, two are one white/1 black, 1 is 2 black. Since the spy randomly chose, there was a 50/50 chance of picking the black ball for the 2 white/black, and a 100% chance for the two black; For the remaining 36 choices, there was a 100% chance of chosing the black ball. So the denominator is really 38, of which 13 are 2 black; 13/38 probability. (this is the one I’m least comfortable with).
Spy #4 pulls one ball at random, observes its color and number, and reports them to you.
He reported Black-7. But that’s just because we stipulated he did so, thus eliminating only every time the spy didn’t say “black-7”. Therefore, the “black-7” is dependent on the problem itself, gives us no help in the outcome, and the probability of the other ball being black is 1/2.
July 8, 2010 @ 9:13 pm
Ron, yes, I meant JeffJo. That’s what happens when you get old and senile.
July 8, 2010 @ 9:13 pm
JeffJo
Sorry that I didn’t express myself well. I wasn’t clear in my words regarding possibilities and probabilities.
In Foshee’s scenario, we can rule out certain possibilities. GG is not possible. One boy is certain, so we are simply left with a basic 1/2 coin flip. As certainties are arrived at, the area of available possibilities is diminished resulting in a higher probability.
Or to be clearer, maintaining birth order would allow a 1/4 probability for either birth order position which added together brings us back to 1/2.
July 8, 2010 @ 11:23 pm
I think it can be proven that knowing the day of the week that the boy was born is irrelevant. I will attempt an indirect proof, by first assuming that knowing the day of week is relevant and then look for a contradiction:
Another way of saying that the information about the day of the week is relevant is to state that P(B,Tu) – the probability of the second child being a boy given that the first child is a boy born on Tuesday – is not equal to P(B,?) – the probability that the second child is a boy given that the first child is a boy but not being told what day of the week on which the first child was born.
Therefore let us assume that P(B,Tu) and P(B,?) are unequal.
If we know P(B,Tu) we can calculate P(B,?). First, recognizing that P(B,Tu) = P(B,Mo) = P(B,Su) etc. Secondly recognizing P(Tu) – the probability that the first child was born on Tuesday, is 1/7 and is the same value for P(Su), P(Mo), etc.
So P(B,?) = P(Su)P(B,Su)+P(Mo)P(B,Mo)+P(Tu)P(B,Tu)+ … + P(Sa)P(B,Sa)
Since as previously observed, P(B,Tu)=P(B,Mo)=P(B,Su)… the solution for P(B,?) becomes:
P(B,?)= 7P(B,Tu)/7=P(B,Tu)
which contradicts the original premise. Therefore the assumption that the specification of the first boy’s day of birth cannot be relevant.
July 9, 2010 @ 12:17 am
Charles, you do you assume that fathers with a boy and girl never phrase the question using “at least one girl.” The proof has been given on this page, but to see it easily, suppose you went to a big conference in which there are 100 rooms with 100 speakers. Each speaker phrases the problem either “I have at least one girl” or “I have at least one boy….”
In 25, on average, of those rooms the speaker has two girls and must phrase the problem in terms of girls. Similarly, the 25 speakers with two boys must phrase the problem in terms of boys.
What about the remaining 50 speakers with one boy and one girl? Suppose all 50 of these guys say “boy,” the assumption you deny you make. Then in 75 of the 100 rooms, the speaker says “boy.” In 25 of those rooms, the speaker has two boys, and in the remaining 50 he has a boy and girl. We then arrive at your 1/3 answer: If you walk into the conference, choose a room, and hear the speaker say “boy,” you should conclude he has two boys with probability 1/3, which was your answer.
Suppose instead that half of the 50 say “boy” and the other half say “girl.” Then there will be 50 rooms in which the speaker says “boy.” In 25 of the 50 rooms in which the speaker says “boy” the speaker has two boys and in the other 25 he has a boy and a girl. So you should conclude, given you randomly select a room and hear the speaker say “boy,” that the speaker has two boys with probability 1/2.
I think I agree with all your spy assertions. I don’t understand, though, why you think the boy-girl problem is analogous to a spy who is BOUND to report whether he found a black ball, and then reports the black ball’s number should he find one. The analogy would be: all fathers always tell you if they have at least one boy, and should they have at least one boy, they also tell you the day of birth of one of their boys. You assume in arriving at 1/3 that the probability a father with a boy and girl will tell you anything other than, “I have a boy born on a X” is zero.
Ron: the answer to problem 5 is 1/2, as you can verify by simulation on a computer, or using coins, if you wish.
The spy does reveal something to you: before the spy says anything, you don’t know whether the urn you chose contains at least one black ball. Problem 5 is analytically identical to Problem 1, because Problem 1 specifying that you *randomly* draw a ball from the urn you selected is exactly the same as problem 5 telling you that the spy *randomly* (by coin flip) chooses to reveal “black” or “white” when she can truthfully reveal either.
To see that physically revealing a ball does not pin down the probability the other ball is black to 1/2, imagine the spy doesn’t look into the urn and utter a sentence, instead she looks into the urn and physically shows you one of the balls therein. Suppose further the spy enjoys showing you black balls and does so whenever she can. You choose an urn and she physically shows you a black ball. You should conclude the other ball in the urn you chose is black with probability 1/3, not 1/2.
July 9, 2010 @ 12:28 am
Sorry, I’m the immediately preceding anonymous poster.
July 9, 2010 @ 12:29 am
I’m not a mathematician, but a lawyer, so while I’m not used to figuring out probabilities, I am used to parsing language. It seems to me the obvious answer is 1/2 as the information about being born on Tuesday is irrelevant.
Parent has told us he has one child. We know that child is a boy. What is the probability that the other is a boy? Simple; the same as the probability that any child in the population is a boy, 1/2 (I understand technically this is something more like .515, but I’ll use .5 for simplicity’s sake). The unknown child’s sex is independent of the other’s sex.
Now if the question were: I have two children. What is the probability that I have two boys? Then the answer would be 1/3.
Like I said, I’m no mathematician, so someone please tell me if I’m wrong, but I don’t see how Tuesday is relevant.
July 9, 2010 @ 1:23 am
Okay, I just re-read my previous comment and thought it poorly written. To clarify my position:
To the question “I have two children; what is the probability that they are both boys?,” the answer is clearly 1/3 since the possible outcomes are: BB, BG, GG.
But that’s not the question being asked in the problem. Since we know one of them is a boy already, the question is really, only about the one unknown child, not the set. Or to put it otherwise, since we know one is a boy, GG is no longer a possibility and the only remaining possibilities are BB and BG. Thus, the chances are 1/2 that the other is a boy.
I think a lot of the math people on here are making it more complicated than it needs to be by reading too much into the question. And I still don’t think Tuesday is relevant.
July 9, 2010 @ 2:00 am
Decided to wade in again, despite the possibility of drowning quickly.
Someone please tell me what’s wrong with this approach:
The problem is “I have two children. One is a boy born on a Tuesday. What is the probability I have two boys?”
So we imagine two children. We know one of them is a boy born on a Tuesday. What are the possible two-child families, given that one child is known to be a boy born on a Tuesday?
They are the 7 combinations of a boy born on a Tuesday matched with a boy born on any of the 7 days of the week, and the 7 combinations of a boy born on a Tuesday matched with a girl born on any of the 7 days of the week.
So there’s 14 possible outcomes. And 7 of them are two-boy families. 7/14 = 1/2 = the answer that common sense gives you.
Voila? QED?
July 9, 2010 @ 4:47 am
SCHC,
There are two birth events in a two child family. In the first you end up with a girl or a boy. For EACH of these two possible birth events there is a second possible birth event, which could also be a boy or a girl.
So the four equal probabilities are Boy Boy, Boy Girl, GirlBoy and Girl Girl. Those of us that believe the answer to the simple question is 1/3 simply remove the GirlGirl element.
This leaves three equally probable outcomes of BoyBoy BoyGirl and GirlBoy.
July 9, 2010 @ 8:53 am
Chris,
I am happy to accept that Problem 5 IS a reveal situation if you assure me that it is. I’m not sure of the relevance to the Foshee problem, however.
The Foshee problem most definitely does NOT have a reveal element to it.
July 9, 2010 @ 9:01 am
It’s getting complicated with so many people arguing, when very few pairs say the same thing. Here are some points addressing several of them, ending with what may be my last contribution here. I can’t keep repeating the same things:
1) In probability, there is a concept called isomorphism, where you change the actual random process into an equivalent one. This can make it easier to count things, or apply conditions. We often do it without realizing we are. Sometimes it even isn’t clear which is correct and which is the isomorphism.
2) We make an original problem smaller by treating its condition as though it is part of the random process itself, which is very wrong to do in general but can be a valid isomorphism if done carefully.
Example: Just like we consider GG because it is a possible two-child family type, we technically should consider three-child family types. But that complication adds nothing, so we ignore it. We create a subset of the problem “the father has a random set of children” with a smaller, simpler one where he must have exactly two. We treat the condition “has two children” as part of the imaginary, isomorphic random process.
Notice that once we do that, we are always dealing with an isomorphism. There is no process that we can say is the “real” random process in our solutions.
3) Is the “random occurrence” in Foshee’s problem the birth of two children, or the selection of a man? If handled properly, it doesn’t matter as they are isomorphisms of each other. But we can’t easily apply the conditions we have to two individual births, while we can apply them to the selection of one man with the possible family types that include two children. We use the randomness of births to define the probabilities for each of those types, not as our random occurrence.
4) The gist of this probability problem is matching properties with children. The fundamental difference in this discussion, is identifying whether the problem is talking about the non-specific property of a specific child, and if it is talking about a specific property of a non-specific child in the pair.
In my “spy” examples, when the spy looks at the contents of an urn with some combination of the values “black” and “seven” already in mind, his statement about that specific property of a non-specific ball. This is true even if only one ball has the property; he *knew* what property he wanted in advance, and *required* a ball in the pair to have it before making his statement. He didn’t care which ball had it. When he picked a ball at random and observed a property that ball had, his statement was about a non-specific property of a specific ball.
There are several other ways to create this difference, that are all isomorphic. If the spy shows us a ball (a “reveal”), the statement is about a specific ball. But it is still an identical problem to when he looked at it without a reveal, and told us about it.
If you use the isomorphism of selecting a man from all men who have family type BB, BG, GB, you are finding a specific property of a non-specific child. It is easy to see that this was done in the solutions above, and when Ron wanted to count only 147 squares. That’s why I said the man is required to have the specific property “one son is a Tuesday Boy.” You can make it a non-specific property of a specific child by letting the man decide what to tell you. In that case, you have to divide some cases in half; those where only one of the two has the non-specific value that was mentioned.
Chris’ blue houses in problem #3 represent a specific property, but in problem #4 they are represent a specific child. The pink houses are also about a specific child in Problem #4, but in Problem #3 pink houses fit in neither category. Which is part of the issue Chris has with Foshee’s answer.
5) Ron is interpreting Foshee’s statement as three separate statements: (A) “I have two children.” (B) “A non-specific child has the specific property ‘boy.'” (C) “A specific boy has the non-specific property ‘born on a Tuesday.'” That way, it is isomorphic with my Spy #2, and the answer is 1/3.
6) But look closer at the original statement, and how Ron is subdividing it. The word “boy” appears only once, but Ron has given it different contexts in the two statements he extracts. There is no specific boy Foshee is talking about in statement B, but it is a specific boy in C. This is Ron’s logical fallacy. The same word can’t be both specific and non-specific at the same time.
Said another way, “a specific property P belongs to a non-specific child” is isomorphic with “one unrevealed child must have property P,” while “a specific child has non-specific property P” is isomorphic with “reveal a child and see it has property P.” So Ron, your interpretation is not “revealing” that the child is a boy, but is “revealing” that the child is a boy born on a Tuesday. You can’t do both.
And it won’t help to re-explain how you get to your answer. Chris and I get that. What we don’t get is how you can think the boy is non-specific when you read the sentence from the start to that word, but specific when you read it from that word to the end.
7) Gary Foshee is doing the exact same thing Ron is, except backwards. Ron accepts intuition while rejecting the assumption that all information is applied the same way. He makes “boy” both specific and non-, whether or not that is logically sound, and gets an answer that looks nice but can’t be justified. Foshee accepts the assumption while rejecting intuition. He applies all the information the same way whether or not that way is mathematically sound, and gets an answer he feels is justified so it doesn’t matter that it looks weird.
8) There is a way to resolve this that is both mathematically and logically sound. Accept that the statement is 100% non-specific information about a specific child, because there is no reason why Foshee could not have mentioned a girl if he had one. So the condition is not “One is a boy (born on a Tuesday),” but “I choose one to mention randomly: he is a boy (born on a Tuesday).” Ron’s interpretation about the added information clearly indicates he thinks such a selection happened.
But then the answer is 1/2 regardless of the added information. Which is what everybody seems to want.
July 9, 2010 @ 5:52 pm
JeffJo,
Here is what Foshee actually said.
“I have two children. One is a boy born on a Tuesday.”
So much analysis for such a simple statement. I do believe that you are more interested in my solution than I am, JeffJo!
You need not worry I am going to repeat my argument. It is somewhere above at least once, and I stand by it until someone comes up with an argument I can understand that proves me wrong.
July 9, 2010 @ 8:50 pm
You have to try to understand it first. So far, you haven’t.
There are two pieces of information in that statement. They apply the same way. You apply them diffferently. What is so hard about seeing that is wrong?
July 9, 2010 @ 9:52 pm
Ron, obviously the reveal in the puzzle is the revelation that the father has a boy, or a born boy on Tuesday in the variant. Problem 5 is exactly the same as the simple boy-girl puzzle except that problem 5 tells you what the revealer (spy/father) does in all states of the world. We need to know that to answer.
SCHC, there are three types of families: two boys (BB), two girls (GG), or mixed gender kids (M). But they aren’t equally likely: three possibilities does not imply the probabilities are all 1/3.
If we took the kids in a given family and stood them side by side in no particular order, we would be equally likely to see any of: GG, BB, GB, or BG. The last two are both mixed gender families, so we are twice as likely to encounter an M family than a BB family.
When the father tells us that he has a boy, it is true that we can infer that he does not have two girls. But we should also usually change our beliefs over the probability he’s a BB relative to an M. Search the page for “billion” and try my problem about overcrowded housing to see that.
July 10, 2010 @ 12:52 am
Chris,
Your definition of “reveal” is different to mine. See my comments on your Problems 3 & 4 above (#’s 80 & 86).
Re your answer to SCHC above, when you take away the GG from the four possible family outcomes of BB BG GB and GG, the three two child units that remain are all equally likely.
Why should we “change our beliefs over the probability he’s (sic) a BB relative to an M”?
Reference to your “billion” problem doesn’t help. Here it is:-
” There are four houses. House A contains a billion boys. House B contains a billion minus one boys and one girl. House C contains a billion minus one girls and one boy. House D contains a billion girls. You walk up to a house, you can’t tell which, ring the bell, and a boy answers the door. What’s the probability you’re at house A?
The people insisting the answer to the boy-girl problem is 1/3 might answer: Since a boy answered, I cannot be at house D. There are three remaining possibilities, one of which is house A, so there is probability 1/3 I chose house A.
In this version of the problem, though, it should be easier to see why that reasoning generally fails. Given a boy answered the door, is it equally probable you’re at house A or C? What odd assumption about which kid opens doors in houses with at least one boy and at least one girl makes it equally likely we’re at A, B, or C, given a boy answered the door?”
I don’t think ANYONE would answer a 1/3 probability of House A, let alone “the people insisting the answer to the boy-girl problem is 1/3”
It is true you can rule out house D. But the weighting in the other houses is so massively biased towards one sex or the other that it bears no comparison to the simple question where the three remaining family possibilities BB BG and GB are three of the four equally probable outcomes reuslting from two birth events.
God knows what unnatural sequence of events would have produced the four houses you describe.
July 10, 2010 @ 8:56 am
Ron, if you see that in the billions of kids problem the answer is not generally 1/3 because the sex ratios in the remaining houses are not equal, you should see that that is also true in the boy-girl problem. The only difference is how dramatically the sex ratio differs across the remaining households.
In both cases the answer actually is 1/3 if and only if we assume that only boys answer the door in mixed gender houses, or that fathers with mixed gender kids always reveal that they have a boy.
Anyways, I thank you for taking the time to try to explain how you reason about these problems.
July 10, 2010 @ 7:32 pm
Chris,
You said:-
“In both cases the answer actually is 1/3 if and only if we assume that only boys answer the door in mixed gender houses, or that fathers with mixed gender kids always reveal that they have a boy.”
In the simple question and the Tuesday Boy problem, the fathers with mixed gender kids ALWAYS DO reveal that they have a boy.
So both answers are 1/3.
Agreement at last.
July 11, 2010 @ 10:38 am
As you said before, Ron, if there is a “reveal” the probability is 1/2. It can only be 1/3 if you “reveal” Tuesday but not “boy.” That’s what I’ve been trying to get into your head for several weeks.
July 11, 2010 @ 12:24 pm
JeffJo,
As I said in 104 above:-
“Chris,
Your definition of “reveal” is different to mine. See my comments on your Problems 3 & 4 above (#’s 80 & 86).”
As for the rest of your comment, I can only suggest you have a debate with Chris about the circumstances where 1/3 is the right answer.
You say:
“It can only be 1/3 if you “reveal” Tuesday but not “boy.”
Chris says:
” the answer actually is 1/3 if and only if fathers with mixed gender kids always reveal that they have a boy.”
AsI said before I agree with Chris.
July 11, 2010 @ 11:14 pm
Ron, to be clear: I do not disagree with anything JeffJo has said.
I also do not understand how you somehow manage to read the puzzle as telling you to assume that no father could conceivably say “one is a girl” rather than “one is a boy,” but this no longer a question of statistical reasoning.
July 11, 2010 @ 11:34 pm
Chris,
I agree that this is no longer a question of statistical reasoning.
There seem to be two different disputes here.
1. In the “statistical expert ” community there is a disagreement about whether the answer to the “simple” question is 1/3 or 1/2. You and JeffJo appear to be in the 1/2 camp whereas Foshee, Bellos, Devlin and others are in the 1/3 camp. As a layman, I can see both arguments.
2. Is the answer to the Tuesday Boy question different to the answer to the “simple” question. I am only really interested in explaining why I feel the answer is “no”.
I think JeffJo and you agree that the answer is no, but JeffJo says that if the answer to the simple question is 1/3 then the answer to the Foshee question is 13/27.
I disagree and have explained why the Foshee method of calculation is flawed
It’s probably best that we leave it there, rather than flog a dead horse.
July 12, 2010 @ 9:17 am
Read Keith Devln’s *second* article. In the community of “applied mathematicians and statisticians” (his words), there is general agreement that the problem as stated is ambiguous but better answered 1/2. The community of “pure mathematicians and puzzle specialists” tends to make an assumption that forces the answers to be 1/3 and 13/27. That assumption is unfounded, which is the only valid point you have made about the “Foshee method of calculation is flawed.”
Your problem is, that you want to make that assumption for just part of the problem, which we have told you repeatly, and you have not commented on. That is where you are wrong. You need to make it, or not.
July 12, 2010 @ 2:43 pm
JeffJo,
I refer you to the answer I gave at #65.
The horse is dead – lay down your whip, take a deep breath, and move on.
July 12, 2010 @ 6:16 pm
It’s dead because you didn’t feed it. You “proved” nothing, only that you could ignore the issue.
July 12, 2010 @ 7:31 pm
I’m an amateur and could use some help: Let’s change the problem:
From a standard deck of cards, two cards are chosen.
Problem 1: What are the odds that both cards are a red suit (hearts or diamonds) given that one of them is a red suit? [answer: 1/3]
Problem 2: What are the odds that both cards are a red suit given that one of them is the ace of hearts? [answer: (26+26-1)/(52+52-1)=51/103; when you are given a specific card, it “anchors” the set of possible events, and removes a dimension or degree of freedom that you have in Problem 1, thus changing the problem.]
Is this analysis correct? The gender and the birthday are independent, just like the color and the suit, no? So, how does independence affect this problem?
July 12, 2010 @ 7:42 pm
As a clarification, my example should be “draw with replacement,” such that you could draw two of the same cards. You draw a card, write down the card, replace it and then draw again, writing down your second card.
I believe I should think of these as two completely separate problems, thereby avoiding confusion/conflation.
Problem 1 involves a 2×2 grid, since there are two possible outcomes to each draw, red and black. [answer: (n/2 + n/2 – 1)/(n+n-1)=1/3]
Problem 2 involves a 52×52 grid, since there are 52 possible outcomes to each draw. [answer is same formula: (n/2 + n/2 - 1)/(n+n-1)=51/103]
July 12, 2010 @ 8:05 pm
For your own sanity, first think of these as two completely separate problems, and get comfortable with the solutions.
Then, if you want to bend your mind, you can try to work backwards to see what has really changed from Problem 1 to Problem 2 to make this a difficult issue to wrap one’s mind around.
My gut instinct is that when you’re dealing with small numbers, your instinct and the math diverge. For example with the Monty Hall Problem, if instead of three doors, you had 100 doors, and after picking one of them, Monty opened 98 of the other 99 doors, you would switch in an instant. It’s the same problem, but with larger numbers that clarify the key issue.
When you switch from the suit color (n=2) to the actual individual cards (n=52), it shows you that it’s the formula that matters and the size of “n,” not the color of the cards.
July 12, 2010 @ 8:41 pm
The way I think about it is that the unconditional probability is 1/4, but when you condition on the information you provide, you are restricting the “event space” to a subset comprised of one horizontal stripe on the grid and one vertical stripe.
You only count the intersection of these stripes once because after all, the probability of any single square on the entire grid is the same for all squares. It’s tempting to think that you would count this square twice, but by definition, the first member of each ordered pair is the row, and the second is the column, and so you would no more double-count that event (giving you 14/28=1/2 in the Boy Tuesday problem or 52/104=1/2 in the card version) than you would double count the Boy-Boy square in the 2×2 problem (giving you 1/2 instead of 1/3). If you keep arriving at 1/2, you need to think about what it means to double-count this same event.
July 12, 2010 @ 10:25 pm
Having read some of the debate in the above comment section, I have empathy for both sides. Before formally studying probability, every person has an informal or gut sense of odds and probability. However, these instincts are often proven wrong by the mathematics of probability. When I first took a probability class, I disagreed so strongly with my professor on a problem during the first lecture that I approached him after class. I was so sure of my position that I practically wanted to fight him. I actually never returned and I dropped the class. But after later studying probability, I learned that he was exactly right.
For those (like me) who are fascinated by why the mathematics of probability theory often yields counterintuitive results, what is interesting about this problem is that the probability of two boys begins at 1/4 (no information/unconditional probability of two boys), and as you get more information, the result seems to converge toward 1/2.
One way to explain this is that the key to this problem is to focus on the square in the grid where both the first and the second draw are the same. This is the point where the horizontal and vertical lines intersect in the restricted/conditional set. Every square on the grid has equal weight, and this square should not be double-counted.
As you have a finer partition, you still have a quadrant for Boy-Boy, but it is finely divided. Half of the horizontal line will be in the Boy-Boy quadrant, and half of the vertical line will be in the Boy-Boy quadrant, and half of the horizontal line will be outside of the Boy-Boy quadrant, and half of the vertical line will be outside of the Boy-Boy quadrant. To calculate the conditional probability, you add up the half of the horizontal line and half of the vertical line in the Boy-Boy quadrant, and then divide but the full horizontal line plus the full vertical line; but since they intersect, you have to subtract the double-counted square from both the numerator and denominator. This is the graphical representation of the analytical formula (n/2 + n/2 – 1)/(n+n-1). (Remember, the formula is the same whether n=2 or n=52 or n = infinity).
So, as you are given more information, the partition/filtration of the event space becomes finer and finer, there are more squares on the grid, and each square thus has a smaller probability weight. Suppose you are told more details about the boy, such as hair-color, eye-color, first letter of first name, etc., and suppose all of these attributes are evenly distributed probabilistically across all boys and girls. Then “n” would be very large and you would have a very fine partition. The probability weight of the double-counted square would be smaller and smaller, and analytically this would be reflected by the fact that the 1 subtracted from both the numerator and denominator would become insignificant. As n goes to infinity, the limit of the fraction would be 1/2.
For those paying close attention, my example with the cards was not perfectly analogous to the Boy Tuesday problem. In the Boy Tuesday problem, the birthday (Tuesday) adds one more partition of the data set on top of the gender (boy). In my example, I added two more partitions on top of the suit color (red suit) when I added suit (heart) and card number (ace) on top of suit color.
July 13, 2010 @ 4:42 am
Eduardo approach this from a logic standpoint first. Is your probability likely to be greater or lower when starting with a specific card like the Ace of hearts as opposed to any random red suited card? Yet you have it set 51/103 which is far likelier than 1/3.
On the boy girl problem, lay out a two rows of B G spaced out then draw lines representing the probabilities. You have four lines. BB BG BG GG.
Now erase one G (either one since order is unimportant) and eliminate the lines of probability that link to that G. You eliminate 2 lines leaving 2 lines. The remaining probability for a boy is now 1/2.
In Foshee’s problem, the added information resets the math leaving us with 13/27 which is just slightly less than the 1/2 probability we have when we have less information.
As the others stated, as long as the given information that is revealed is random and not necessary, then we do not have a Monty Hall scenario. If you were free to say black suit instead of red suit then we can use that information to begin in our equation, and simply find for the 2nd card.
Remember that the Monty Hall is associated with three distinct doors, but our problem has 2 doors with 4 interlinked probabilities. When we remove one of the links (G), we remove 2 lines of probability not 1.
July 13, 2010 @ 6:56 am
Eduardo: First a minor nitpick. “Odds” are values used in gambling to determine payoffs. They are expressed differently then probability. A probability of 1/3 means the odds are “1 to 2 for” the event to happen and “2 to 1 against.” If you bet $1 and win, you get your $1 back and $2 more.
Now, rather than just think about your card problem, imagine that you get out a deck of cards count the results until you get 1000 results. You will probably do it without replacement, to avoid the extra shuffles. But you do have one problem: what will you do if the top two cards are black? The probability that both are red is about 1/3 if you don’t count the times when you get two black cards, effectively requiring 1333 shuffles to get 1000 results.
Suppose, instead, that you keep track of two different totals. One for red and one for black. If you get two of the same color, you must count it toward that total. But if you get one card of each color, you draw a third card and count that trial only toward the total of the third card’s color. If you do it this way, the probability is about 1/2. The difference is that in the 1/3 case, you were compelled to count a red+black result for the red total. Here, you choose one color.
The original question is ambiguous, because it does not make it clear which method matches “A random father of two tells you he has at least one boy.” If the father is compelled to tell you about a boy if he has a boy and a girl, the probability is 1/3. But if he chooses one or the other somehow, the probability is 1/2. Chris and I are saying that it is more reasonable to assume the father chose what to say, then that he was compelled.
Now, extend that to your Ace of Hearts example. If you decide ahead of time to only count the cases where you get the Ace of Hearts, the probability is 49/101 (without replacement). If you simply choose one of the top two cards and ask “One of the cards is the three of clubs, so what is the probability I got two black cards?” the probability is the same “about 1/2” it was before. It becomes far more evident that the “choose” method is a more reasonable interpretation this way. In fact, its reasonableness is why people expect the answer to not change.
Ron is doing something completely different. He doesn’t count the cases when he gets two black cards, like in the first method. But when he gets two red cards he chooses one of them and only counts it if he chose the Ace of Hearts. So half of the time he gets it, he doesn’t count it. He won’t explain why he thinks that is a more reasonable match to the problem statement, only that he likes the answer better because it stays at about 1/3.
July 13, 2010 @ 2:27 pm
Sam: If you think about our problem as having four doors labeled BB, BG, GB, and GG, this problem is identical to the Monty Hall problem except in the numbers.
You can model both as a general problem: Suppose that initially there are N=A+B+C equally likely cases. You find out a fact about a trial that is inconsistent with the A cases, consistent with half of the B cases, and consistent with all of the C cases. The probability that the result is any one of the B cases is 1/(B+C/2), and 1/(2B+C) for any one of the C cases.
For Monty Hall, N=3 (which door has the car) and A=1 (the opened door). You get the wrong answer if you assume B=0 and C=2, and the right answer if you assume B=C=1. (B is 1 because if the car is behind the door the contestant picked, Monty could have opened a different door).
For the Two Child problem, N=4 (four family types) and A=1 (GG). You get 1/3 if you assume B=0 and C=3, and you get 1/2 if you assume B=2 and C=1. (B is 2 for the BG and GB types, when the information is randomly determined instead of predetermined.)
July 13, 2010 @ 2:53 pm
Philosophers, logicians, semanticists, linguists, and lawyers will have a problem with the way this problem is phrased. Probabilists and mathematicians will not because this is standard language of conditional probability problems in any probability textbook or class. I learned this the hard way.
The Boy Tuesday problem is a problem of draw with replacement, so any clarifying analysis of it or analogy to it should also involve draw with replacement (balls in an urn, deck of cards, etc.)
The hardest part of probability for me is finding intuition behind the mathematics. Here’s the intuition the way I see it, which goes along with the grid depiction (above in #115):
Problem A:
– I draw two cards
– I tell you that the first card is red
– The probability that both cards are red is 1/2
– This is b/c the probability that the second card is red is 1/2
Problem B:
– I draw two cards
– I tell you that one of the cards is red
– The probability that both cards are red is 1/3
– This is lower than 1/2 because from 1/2 you “subtract” the chance that both cards are “the same” (i.e., both are red). I put “subtract” in quotes because you are removing the double-counting by subtracting 1 from both the numerator and the denominator (formula above in #115).
And the key insight: As you get more and more information about the card (or the Boy), the chances that both draws will be “the same” gets smaller and smaller. This is why information affects conditional probabilities, even when your gut tells you that it shouldn’t matter. (“Everyone must be born on some day, so why does Tuesday change anything?” Use the cards example to remove the human temptation.)
But if I kept telling you infinite details about the Boy until you could uniquely identify him, then the chance of two of that particular Boy (overlap) would be zero, and you would be back to 1/2. In other words, you are no longer dealing with a generic “B”; you have a very specific person, and by telling you WHO this child is, I have effectively turned Problem B into Problem A.
The moral of the story is that more information almost always reduces uncertainty. You can doubt this at your own peril.
July 13, 2010 @ 4:19 pm
Eduardo: Your Problem B is ambiguous, even to Mathematicians and Probabilists. Especially to Probabilists. Its answer depends on why you said “one of the cards is red.”
These problems are not ambiguous:
Problem C:
– I draw two cards
– If they are both black, I keep drawing two until at least one is red
– I tell you that I forced one of the cards to be red
– The probability that both cards are red is 1/3
Problem D:
– I draw two cards
– You ask me “is one of the cards is red?”
– I answer “yes”
– The probability that both cards are red is 1/3
This one doesn’t give enough information, but an answer is still possible, and it isn’t 1/3:
Problem E:
– I draw two cards
– You ask me to tell you the color of one of the cards
– I tell you that one of the cards is red
– The only answer you can give is that the probability that both cards are red is 1/2. It actually depends on why I might choose to say red, but only I know that.
If you are taking probability now, you can prove this. First, note that any answer you give can’t be different if I tell you one of the cards is black and ask for the probability both are black. Call that probability X. Then assume that I tell you that a card is red with probability Y. That is,
P(RR|red)=P(BB|black)=X
P(red)=Y
P(black)=1-Y
Then the law of total probability says:
P(RR) = P(RR|red)*P(red)+P(RR|black)*P(black) = X*Y + 0*(1-Y) = X*Y
P(BB) = P(BB|red)*P(red)+P(BB|black)*P(black) = 0*Y + X*(1-Y) = X-X*Y
So
P(RR)+P(BB) = X*Y + (X-X*Y) = X
But we know that P(RR)=P(BB)=1/4, so P(RR)+P(BB)=1/2. QED.
Note that if the answer was 1/3, that would mean that the probability of two matching cards has to be 1/6.
July 13, 2010 @ 8:27 pm
JeffJo,
I may be a bit behind reading all the comments above, but I think we are saying the same thing.
I say that this is not a Monty Hall type because that would rely on the necessity of the revealed information.
In the Tuesday child, I see the reveal as simple random choice and not a compelled matter. If the father is free to reveal information about either child, that eliminates the Monty Hall archetype and leaves the answer at near 1/2.
Try this one. A man tells you he has flipped 10 coins and 9 are heads. Another man tells you he has flipped 9 coins all heads and is about to flip the 10th. The first man offers you 5 – 1 odds that all 10 of his coins are heads. The second man offers even odds that his 10th flip will be heads. If you must place a wager, with which man do you make the wager? What are the respective probabilities?
July 13, 2010 @ 9:04 pm
If it makes the problem simpler, imagine that an unbiased 3rd party is the one who offers the two wagers, and the coin flipping men are not involved financially in the arrangement. This will remove a suspected motive to the first man’s reason for the information revealed. Assume he was free to state anything.
July 13, 2010 @ 9:10 pm
Sam: It’s called a “conditional probability,” and it’s the same in both problems. It means that some possibilities are ruled out by information you received about ths particular instance of the random process.
In Monty Hall, you learn that the car is not behind Door #3. In Two Child, you learn that GG is not possible. In both, it turns out that a choice involved in how you came by the information is important. Monty Hall has the choice between two doors to open when C1 happened. The father has the choice of two statements to make when GB or BG happened.
July 14, 2010 @ 12:30 am
I don’t want to repeat what I just posted over at Ludologist entirely, but it seems to me that the crucial difference is: does the mother volunteer the Tuesday info, or does the questioner ask it.
In the former case it is merely 100% sample bias and cannot be used to infer anything. In the latter case this is informative because it is easier to answer YES with two boys.
July 21, 2010 @ 4:58 pm
Gary Foshee has fooled a lot of people, me too in the beginning.
The problem can not be solved with conditional probability, that’s a tool only for specialists.
Just Use common probability or Your intuition. That gives You four possibilities:
Boy-known + Boy,
Boy-known + Girl,
Boy + Boy-known,
Girl + Boy-known,
and of course 50% probability for two boys, also if Boy-known is born on a tuesday, is redhaired, has a canary or whatever.
I have tried to convince a danish blog, they still argue.
It seems that the problem is more difficult depending on Your education!
July 27, 2010 @ 8:47 pm
I am in agreement that the solution depends on whether the information provided about the first child is significant, or incidental. A generalized expression of the solution would be as follows:
Let a=the probability that the first child being a boy is significant.
Let b=the probability that Tuesday is significant.
Then
P=ab(13/27)+a(1-b)(1/3)+(1-a)b(1/2)+(1-a)(1-b)(1/2)
July 29, 2010 @ 6:26 am
Place a coin random on a table showing tails.
It’s a coin made on a tuesday (or whatever).
Toss another coin, it lands randomly on the table.
What is the probability that both show tails?
I hope you agree in 1/2%.
Let the coins be children.
Let the first coin be a boy born on a tuesday.
Let the table be the possibilities young and (perhaps) elder child.
What is the probability that both children are boys?
I don’t see any difference between this and the
Gary Foshee puzzle.
My answer is 1/2%.
I wonder if Keith Devlin still think it’s 1/3!
July 30, 2010 @ 5:58 pm
1/2% = 1/2
July 30, 2010 @ 6:03 pm
Preposterous. The answer is 1/2.
August 11, 2010 @ 12:30 am
[…] Decision Science News has a cool graphical explanation for the problem – they also arrive at 13/27 […]
September 2, 2010 @ 7:47 am
I must praise JeffJo for explaining the problem in a much more eloquent way that I had managed in trying to introduce people to it. The intricacies of the question are indeed vital and the concept of the B and T probabilities helps clarify where the disagreements arise.
The only place I may be willing to disagree is that B MUST equal T. This is because, knowing how people converse, it is much more likely that I will discover randomly that someone has a son than discovering their kid was born on a Tuesday. The random discovery aspect is important as I do not believe somebody is twice as likely to mention in coversation that they have a son just because they have 2 sons. I am willing to be argued down on this but I believe that this does give a defense of the inconsistencies in the values of B and T- thoughts?
November 19, 2010 @ 4:43 pm
[…] The Information Grid from the surprisingly popular Decision Science News post Tuesdays’ Child is Full of Probability Puzzles […]
December 8, 2010 @ 7:46 pm
Thanks for the cookie, Andy. 🙂
Maybe I didn’t say it explicitly, but I too believe that B must equal T. I was emphasizing what happens when they are different, to try to explain why people do not initially expect the 13/27 answer. Essentially (and this comes up a lot in this post), we have no reason to treat the two facts differently, so we must treat them the same. It was for this reason that Gary Foshee’s insists T must be 1, since the accepted answer without “born on” information is that B=1.
But the issue you refer to isn’t quite that “somebody is twice as likely to mention in conversation that they have a son just because they have 2 sons,” even though it reduces to that. It is really two issues. First, are they more or less likely to mention one the gender of one child when they have a mixed-gender family rather than a single-gender family? If they are, there is no way we can answer the question since we don’t know by how much the probabilities differ. Puzzles often leave details like that out, for brevity, and we really can’t assume anything except that these two factors are independent. Second, are they more or less likely to mention a boy this way, than a girl, when they have a mixed gender family? And again, by how much? That’s where my factor B comes in. If the problem doesn’t say or imply a value, we have to assume here, too, that there is no difference, and B=1/2.
The problem is, mathematicians and puzzle designers seem predisposed to believe there is an implied value for this problem, or that there should be and it is B=T=1. Look up Keith Devlin’s (of the blog Devlin’s Angle) response to it last May. He says, essentially, that as worded we really should have used B=T=1/2; but if the problem is worded “given the man has a boy born on a Tuesday,” we should use B=T=1. I think that also is wrong.
The mistake Devlin is making is of taking how we read the expression P(E|C), as “the probability of event E given event C.” He applies a magical implication from the word “given” corresponding to this colloquialism. He overlooks that the expression really means “the probability event E happens, given that the outcome is constrained to event C AND UNCONSTRAINED WITHIN EVENT C.” Other fields of math don’t care what happens when the stated conditions aren’t met, so this difference never comes up there. Probability does, but we misuse the word.
There is a lot of extra meaning in the fact that capitalized part. For example, like I said before, if “given” provides this meaning, then in the Monty Hall Problem, “given that Monty Hall opened Door #3 to reveal a goat” means that Monty opened Door #3 BECAUSE it had a goat, regardless of the other unchosen door. This makes the probability that the contestant’s door already has the prize 1/2, and I doubt Dr. Devlin would agree that “given” implies that.
December 14, 2010 @ 12:35 pm
[…] you sya "tuesday's puzzle", was the girl born on a tuesday ? I have two children. One is a boy born on a Tuesday. What is the probability I have two […]
May 17, 2011 @ 9:26 am
I only came across this problem for the first time about a week ago. But I have seen and understood a few similar problems. The interpretation of the question is crucial. I assume that the understanding is that the starting point is to consider all possible families (with the assumption that the gender probability is 1/2 and independent of the gender of any siblings). We discard all families that don’t have two children. I note that everyone does that automatically and without noticing that they’ve actually used conditional probability (in this case we’re given that there are two children). In this (idealised) problem, we also assume that it is equally likely that a child could be born on any day of the week. That gives 196 equally likely combinations of two children families. The families that correspond to at least one boy born on a Tuesday form a cross (formed by one row and one column). That cross consists of 27 equiprobable cells (because they were equiprobable before we starting examining the subset). Of those 27 cells, only 13 correspond to two boys. So the probability sought is 13/27.
If the question had been phrased more like “I have two boys, one was born on a Tuesday, then what is the probability that the OTHER is a boy?”, then the semantics have changed – in fact you have been given more information, because a particular child has been singled out (in my opinion, of course). But (IMO) the original question has been deliberately phrased so as to not be referring to a particular child. That, I believe, is at the heart of why people get confused about the answer.
Of course, some people get confused because they haven’t got a clue about what’s really being asked. When I posted this problem, someone in an attempt to lampoon it, suggested that you may as well ask what if one of the boys had a tentacle growing out of his head? I responded that if the probability that a boy has a tentacle growing out of his head is p, then the probability of there being two boys = (1/2)(1-p/2)/(1-p/4). That varies from 1/3 to 1/2 as p varies from 1 to 0.
On the Tuesday not mentioned version of the problem, a typical attitude is that you know for sure that one child is a boy, so the other being a boy/girl is 50-50. But this would be equivalent to only looking at families where you only (initially) sampled one of the children and didn’t examine the second one if the first was a girl. You’d then be excluding mixed gender families that you shouldn’t have excluded.
October 16, 2011 @ 9:49 pm
Aaargh! That’s still not clear enough. The interpretaion of the thoughts of the information giver is important. If you believed that a particular child was being referenced, then you’d be right to go for 1/2. But that would be boring, and for that reason, I’d choose to assume that, that no particular child was being referenced was the interpretation that you were supposed to be using. For the simpler (non Tuesday version), you could use more transparent phrasing (and possibly kill the amusement of the ensuing arguments) by saying “I have two children, they’re not both girls. What is the probability that I have two boys?” That way it is harder to justify that a particular child was being referenced. I can’t think up a similar phrasing for the Tuesday birth though.
In summary, the problem is largely posted because of the seeming paradox when you get 13/27 or 1/3 as the intended (correct) answer. The problem only really works because we don’t normally expect people to give very precise spoken (or written) statements, and so we have a tendency to extrapolate what was actually meant.
October 16, 2011 @ 10:21 pm
I completely goofed my alternative question. I wrote,“I have two boys, one was born on a Tuesday, then what is the probability that the OTHER is a boy?” I had meant to have said, “I have two children. One is a boy who was born on a Tuesday. What is the probability that the OTHER is a boy?” That leaves almost no room for doubt that a particular child was in the speaker’s mind.
I’m sorry about that becoming three posts.
October 16, 2011 @ 11:30 pm
We have a girl and me and my wife want to have a boy next there are any way that the gender can be decided? Any particular tips?
November 3, 2011 @ 10:01 pm