Is there a problem with most people rating themselves above average?
OVERCONFIDENCE?
One of the most enjoyable types of academic exchange is that of type 17a, in which one group of scholars argues that a psychological tendency is irrational and another group argues that the same tendency is reasonable. It can be even more fun when the groups belong to different fields. If these two assertions are true, we are in for a treat this week as DSN has become aware of a working paper by economists Jean-Pierre Benoît (London Business School) and Juan Dubra (Montevideo) that finds nothing wrong with the idea that most people rate themselves above average.
ABSTRACT
Many studies have shown that people display an apparent overconfidence. In particular, it is common for a majority of people to describe themselves as better than average. The literature takes for granted that this better-than-average e¤ect is problematic. We argue, however, that, even accepting these studies completely on their own terms, there is nothing at all wrong with a strict majority of people rating themselves above the median.
LINK
Overconfidence? http://www.najecon.org/naj/cache/122247000000002148.pdf
It is interesting to see the term “nothing wrong” in the abstract. Decision Science News enjoys papers of type 17a, but it feels that there is too much focus on what is rational / irrational / right / wrong and too little focus on models that capture what people do: the overconfident, the underconfident, and the calibrated. After all, right or wrong are all defined with respect to normative standards, and such norms 1) change over time and 2) are often borrowed from fields (such as probability and statistics), that don’t speak with a single normative voice, but comprise multiple (often irreconcilable) views.
Figure credit: Pilot study by Lionel Page and Dan Goldstein
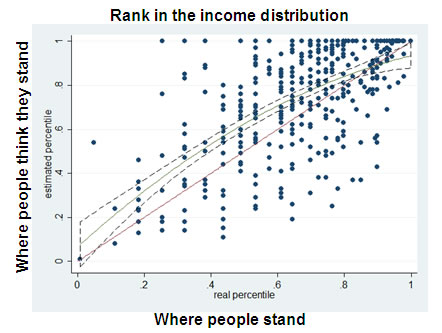


There seems to be heteroscedasticity in the regression – the variance tends to be larger when the real percentile is around 0.5. I’m very interested in the data behind the graph; do you have the original data?
November 27, 2008 @ 4:18 am
Hi Yihui Xie,
Good to hear from you again! Check your email. – Dan
November 27, 2008 @ 3:37 pm
Thanks very much, Dan. This survey reminded me of another one (I’ll implement it in R soon), haha
November 29, 2008 @ 12:31 pm
Dan: I’m with Yihui. The graph does not support the idea that everyone thinks they are above average. A better storyline is: people in the middle have great difficulty placing themselves (large variance) while very rich and very poor people know their place in the distribution.
December 12, 2008 @ 6:35 am
Not sure if my leg is being pulled, but I’ll bite. First I’d say that the graph is not supposed to show that everyone thinks they are above average. Second, to be with Yihui here, you would be of the opinion that the regression might have heteroscedasticity issues, but would not necessarily be of the opinion that the graph does not show overestimation. Lastly, concerning the idea that people at the ends are calibrated and people in the middle simply have higher variance, it seems that at every quintile (in fact at nearly every point on the x-axis that has data), there are more points above the diagonal than below it. There’s increased variance here, but either a) it is not centered around the diagonal or b) a highly improbable event has taken place. I was happy to find that this tendency is less at the extreme ends, though the 0,0 point doesn’t really count since it doesn’t require estimation to know that other people can’t earn less than you do if you earn zero.
December 16, 2008 @ 12:33 am
Reading what I wrote last time, I find the phrase “does not support” is too strong. On average, there are more points above the diagonal indicating over-estimation.
I was trying to point out that a different feature worth exploring is the high variance of estimation. I think a hypothesis may be that the ability to estimate is dependent on where one is in the income distribution.
This reminds me of the “global warming” situation: while a lot of attention is placed on the average rise in temperatures, I’d think that the rise in variability (more extremes) should get more attention.
December 17, 2008 @ 5:57 pm